Cálculo integral con GeoGebra

En nuestro tutorial de hoy, vamos a sumergirnos en cómo calcular la integral indefinida de una función utilizando GeoGebra, presentado a través de un ejemplo minuciosamente detallado.

Empecemos por lo fundamental: ¿Qué es una integral indefinida? Integrar una función, tal como f(x), implica encontrar otra función, g(x)+k, $$ \int f(x) = g(x) + k $$ en la cual la derivada D[g(x)+k] nos reconduce a la función original f(x). $$ D_t[ g(x) + k ] = f(x) $$

Introduce una función en GeoGebra para comenzar. Para nuestro caso, utilizaremos la función f(x)=x².

Procede usando el comando Integral().

En los paréntesis del comando, indica la función que deseas integrar, que en este ejemplo hemos denominado "f".

GeoGebra entonces efectuará el cálculo y mostrará la integral indefinida como g(x)=1/3·x³ para la función f(x) seleccionada.

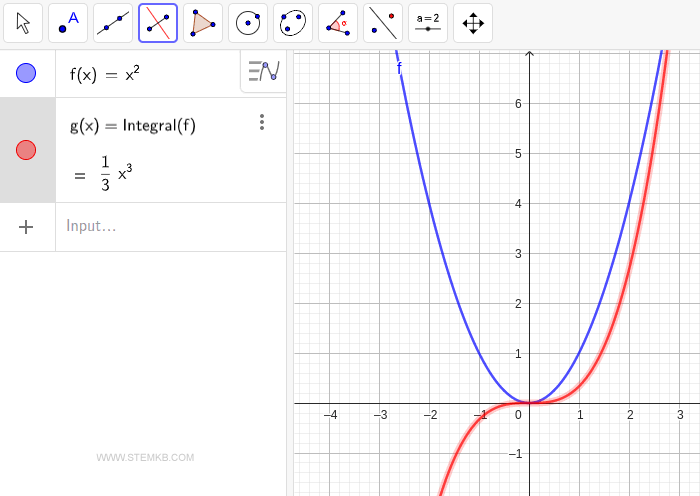
Es crucial comprender que el resultado de una integral indefinida no es una única función g(x), sino más bien una familia de funciones, g(x)+k, donde k representa una constante arbitraria. Esto quiere decir que una formulación más exacta sería g(x)=1/3·x³+k. Este concepto se fundamenta en que la derivada de cualquier constante k es siempre cero, es decir, D[k] = 0. Así, derivadas como D[1/3·x³+2] o D[1/3·x³+3] siempre nos devolverán a la función original f(x)=x².

¿Quieres una confirmación?

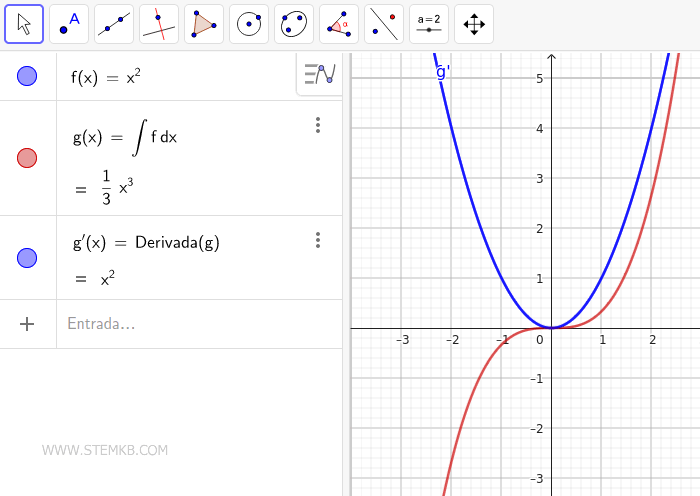
Valida tus resultados calculando la derivada con el comando Derivada().

Para g(x)=1/3·x³, calcular la primera derivada nos retorna a nuestra función inicial f(x)=x², demostrando que la diferenciación actúa como la operación inversa de la integración.

Si esta guía te ha parecido esclarecedora, te invitamos a explorar nuestros próximos tutoriales para ampliar tus conocimientos.