El producto cruz en Geogebra

En este tutorial, te voy a mostrar cómo calcular el producto cruz (producto vectorial) entre dos vectores utilizando Geogebra, de una forma sencilla y eficaz.

Comenzaremos creando dos vectores dentro de un espacio tridimensional.

Para el primer vector, tenemos las coordenadas

$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} $$

Mientras que para el segundo vector, las coordenadas son

$$ \vec{u} = \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix} $$

Si no estás seguro de cómo proceder para crear un vector, te invito a revisar nuestra lección en línea sobre cómo crear vectores con Geogebra.

Luego, solo tienes que introducir ProductoVectorial(v,u) en el campo de comandos de Geogebra y presionar enter.

Recuerda que u y v son los nombres de los vectores que acabas de diseñar.

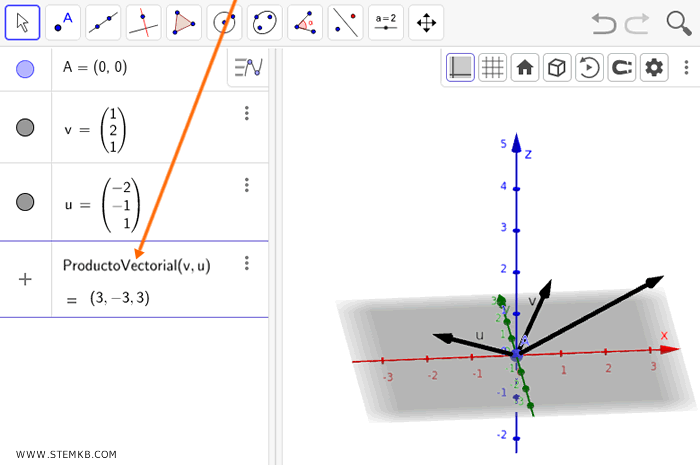
De manera inmediata, Geogebra realizará el cálculo y te mostrará el producto cruz de tus vectores.

Para este ejemplo, el producto cruz resultante es el vector w, cuyas coordenadas son las siguientes.

$$ \vec{u} = \begin{pmatrix} 3 \\ -3 \\ 3 \end{pmatrix} $$

¿Cuál es la importancia del producto cruz? El producto cruz entre dos vectores u y v genera un tercer vector w, el cual se ubica perpendicularmente con respecto a los dos vectores originales. La orientación de este vector resultante se define según el orden de los vectores iniciales. Si los vectores originales tienen la misma dirección, el resultado será un vector nulo. El valor absoluto del producto cruz nos da el área encerrada por los dos vectores en su plano común.

Si este tutorial práctico de StemKB te ha resultado útil, te invitamos a seguir explorando con nosotros.