Conjugado complejo en Octave
En esta lección, explicaré cómo encontrar el conjugado de un número complejo en Octave.
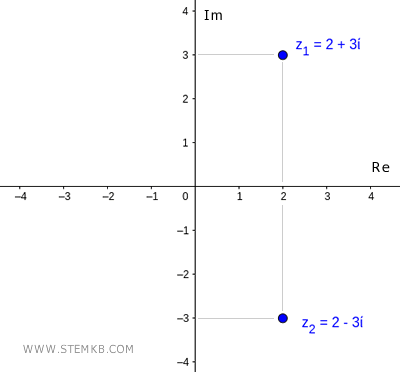
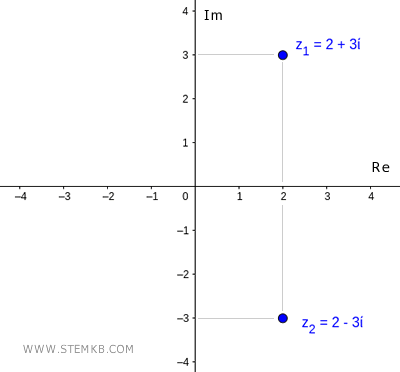
¿Qué es el conjugado complejo? El conjugado de un número complejo z=a+bi es un número complejo que tiene la misma parte real y la parte imaginaria cambiada de signo. Por ejemplo, el número complejo z1=2+3i tiene como conjugado complejo z2=2-3i, y viceversa.
Déjame darte un ejemplo práctico.
Define el número complejo z = 2 + 3i en Octave utilizando la función complex(2,3).
>> z=complex(2,3)
ans = 2 + 3i
Para obtener el conjugado de un número complejo en Octave, puedes usar la función conj().
Por ejemplo, si tienes un número complejo z=2 + 3i, puedes encontrar su conjugado escribiendo conj(z)
>> conj(z)
ans = 2 - 3i
La función devolverá el conjugado del número complejo, que en este caso es 2 - 3i.
¿Cuál es el propósito de calcular el conjugado complejo?
Calcular el conjugado complejo simplifica ciertas operaciones en la aritmética de números complejos.
Por ejemplo, el producto de un número complejo con su conjugado es igual al cuadrado de su magnitud.
Para calcularlo, multiplica el número complejo z por su conjugado conj(z). El producto es igual a 13.
>> z*conj(z)
ans = 13
Para calcular el módulo del número complejo z, puedes usar la función incorporada abs() en Octave.
El resultado de aplicar esta función a z es aproximadamente 3.6.
>> abs(z)
ans = 3.6056
Además, calcula el cuadrado del módulo de z.
El resultado siempre será 13.
>> (abs(z))^2
ans = 13.000
Esto implica que el módulo de un número complejo también se puede obtener tomando la raíz cuadrada del producto del número complejo y su conjugado.
>> sqrt(z*conj(z))
ans = 3.6056
Si encontraste útil la lección de Nigiara sobre el uso de números complejos en Octave, asegúrate de seguirnos para más.
Nota. En el contexto de los números complejos, "magnitud" y "módulo" a menudo se usan indistintamente para referirse al valor absoluto o la distancia de un número complejo desde el origen del plano complejo.