┴ngulo y m¾dulo de un n·mero complejo en Octave
En esta lección, explicaré cómo calcular el ángulo (argumento) y el módulo de un número complejo en Octave.
¿Qué son el módulo y el ángulo de un número complejo? Cada número complejo z = a + bi puede representarse en el plano complejo con las coordenadas (a, b).
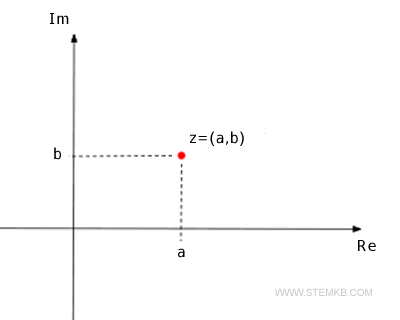
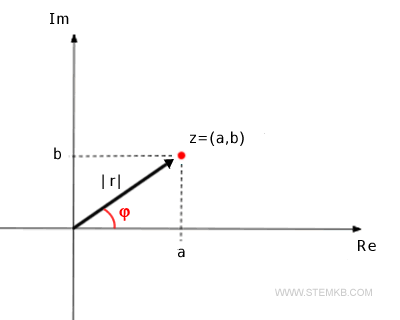
Así que, cada punto en el plano es un número complejo diferente y se puede llegar de forma única desde el origen a través de un vector. La longitud r = |z| del vector se llama módulo del número complejo z. El ángulo φ del vector medido en sentido contrario a las agujas del reloj desde el eje real positivo (Re) se llama argumento del número complejo.
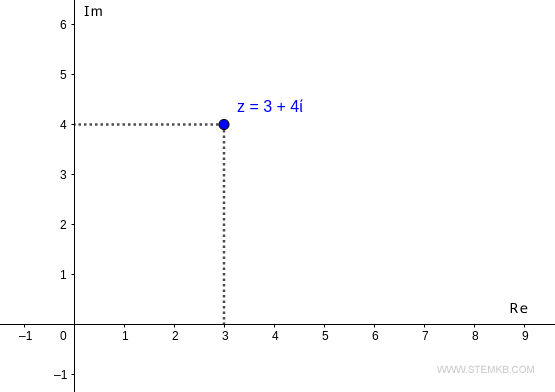
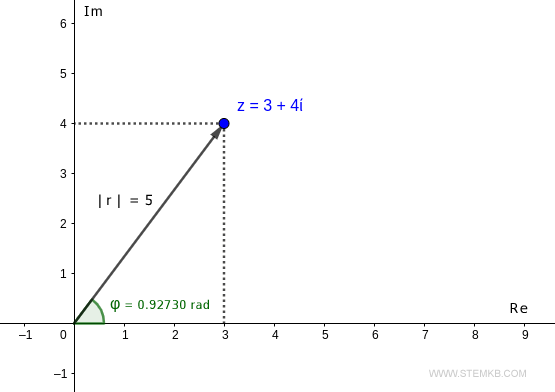
Por ejemplo, consideremos el número complejo z=3+4i
En el plano complejo, el número z se encuentra en el punto con coordenadas (3,4).
Este punto es alcanzable desde el origen por solo un vector de longitud r y ángulo φ.
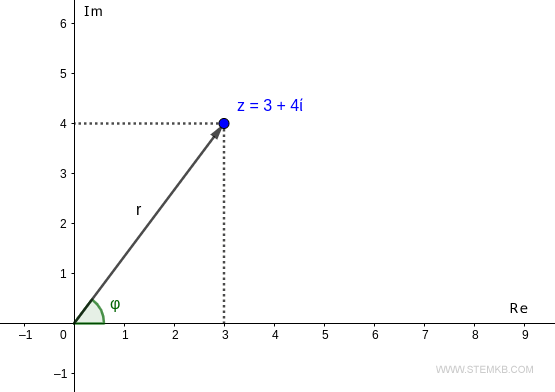
Para calcular el módulo r = |z| del número complejo, que es la longitud del vector, use la función abs() en Octave.
>> abs(z)
ans= 5
Por lo tanto, el módulo del número complejo z = 3 + 4i es igual a 5.
En otras palabras, el vector que conecta el origen con el punto (3,4) tiene una longitud de cinco.

Para calcular el ángulo (argumento) del número complejo, use en su lugar la función angle().
>> angle(z)
ans = 0.92730
Octave devuelve el ángulo en radianes.
En este caso, el argumento del número complejo z = 3 + 4i es 0.92730 radianes, que es aproximadamente 53 grados.
Si esta lección sobre Octave por Nigiara te ha resultado útil, continúa siguiéndonos.