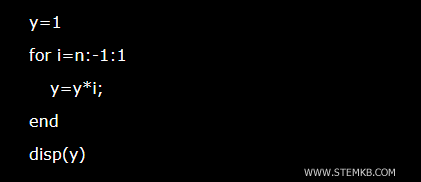Funciones recursivas en Octave
En esta lección, explicaré cómo utilizar la recursión en funciones en Octave.
La recursión se refiere a la técnica de una función que se llama a sí misma múltiples veces. Es un concepto fundamental en la programación funcional.
Para ayudarte a entender este concepto, te proporcionaré un ejemplo práctico.
Puedes usar la recursión para calcular el factorial de un número.
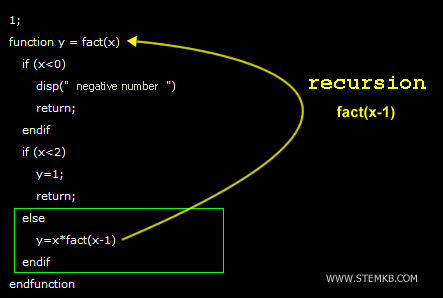
1;
function y = fact(x)
if (x<0)
disp("negative number")
return;
endif
if (x<2)
y=1;
return;
else
y=x*fact(x-1)
endif
endfunction
En este script, he definido una función llamada fact() que toma una entrada numérica (x).
- Si x<0
En primer lugar, la función verifica si la entrada es negativa. Si x<0, la función muestra un mensaje que dice que el número es negativo y termina la llamada a la función utilizando la instrucción return. Esto se debe a que el factorial de un número negativo no está definido.

- Si 0≤x<2
A continuación, la función verifica si la entrada es menor que 2. Si 0≤x<2, la función devuelve 1 y termina la recursión. La instrucción return envía el valor 1 de vuelta a la llamada de función anterior, cerrando efectivamente el bucle recursivo.

- Si x≥2
Finalmente, si la entrada es mayor o igual a 2, la función multiplica el número de entrada x por el resultado de fact(x-1). Esto se logra mediante la recursión, donde la función se llama a sí misma con una nueva entrada de x-1, que es el número entero actual x reducido en uno. El proceso se repite hasta que se alcance el caso base de x<2 y la recursión se termina.
En general, esta función proporciona una forma eficiente de calcular factoriales de números enteros no negativos.
Por ejemplo, puedes llamar a la función fact() que acabas de crear y pasarle 6 como parámetro inicial.
El función toma el número de entrada x=6 y calcula recursivamente el factorial.
n=6
y=fact(n);
disp(y)
El script muestra el número 720, que es el factorial de 6!
720
¿Por qué es el resultado de la función 720?
La función se llama a sí misma cinco veces (recursión) pasando un número progresivamente más pequeño.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)
En la última llamada fact(1)=1, la función devuelve 1 porque el valor de entrada (x=1) es menor que dos.
En este punto, la recursión termina y el proceso retrocede cerrando todas las llamadas anteriores.
Si fact(1)=1 entonces fact(2)=2 porque fact(2)=2fact(1)=2*1=2
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)=2*1=2
Si fact(2)=2 entonces fact(3)=6 porque fact(3)=3*fact(2)=3*2=6
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)=3*2=6
Si fact(3)=6 entonces fact(4)=24 porque fact(4)=4*fact(3)=4*6=24
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)=4*6=24
Si fact(4)=24 entonces fact(5)=120 porque fact(5)=5*fact(4)=5*24=120
fact(6)=6*fact(5)
fact(5)=5*fact(4)=5*24=120
Si fact(5)=120 entonces fact(6)=720 porque fact(6)=6*fact(5)=6*120=720
fact(6)=6*fact(5)=6*120=720
Por lo tanto, el factorial de 6! es 720.
$$ 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 $$
Nota. En este ejemplo, he creado una función de factorial para explicar cómo funciona la recursión en Octave. Sin embargo, si solo necesitas calcular el factorial, recuerda que Octave también tiene una función predefinida específica, factorial(x), que es mucho más conveniente de usar. Además, puedes calcular el factorial desarrollando una función basada en la iteración sin usar la recursión, y el resultado siempre será el mismo.