Cálculo de la norma de un vector en Matlab

En esta lección, abordaré cómo calcular la norma, o magnitud, de un vector utilizando Matlab.

¿Qué es la norma de un vector? Se trata de la longitud euclidiana del vector, conocida también como su magnitud. Por ejemplo, la norma euclidiana de un vector en el plano se corresponde con la longitud de la flecha que lo representa.

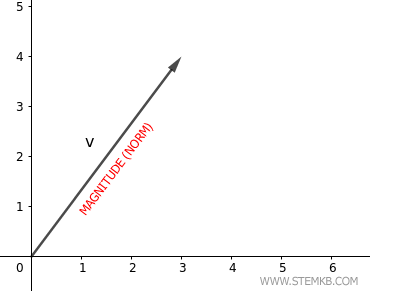
Ahora, veamos un ejemplo práctico.

Tomemos un vector en la variable V

>> V=[3 4]
V =
3 4

Este vector se origina en el punto (0;0) del plano y se extiende hasta el punto (3;4).

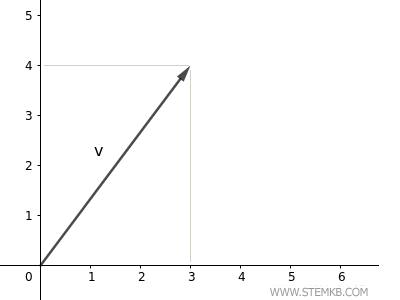
Para calcular la longitud del vector, o su norma, basta con utilizar la función norm(V).

>> norm(V)
ans = 5

Así, la norma euclidiana del vector es 5, valor que representa la longitud de la flecha en el plano.

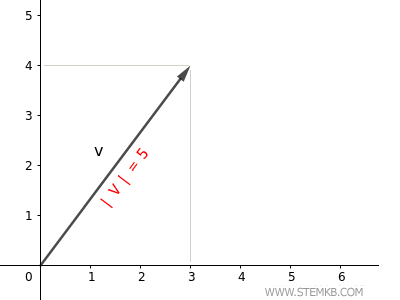
Comprobación. De igual manera, la longitud de un vector puede determinarse aplicando el teorema de Pitágoras $$ | \vec{v} | = \sqrt{3^2+4^2} = \sqrt{25} = 5 $$ Confirmando así que la magnitud del vector es efectivamente 5, corroborando la exactitud del resultado obtenido.