Sistema de ecuaciones lineales en Matlab
En esta clase de Matlab, vamos a explorar cómo resolver un sistema de ecuaciones lineales mediante el uso de operaciones con matrices y vectores.
A continuación, te presento un ejemplo práctico.
Consideremos un sistema de ecuaciones lineales con dos incógnitas, representado por dos ecuaciones.
$$ \begin{cases} x+5y-3 = 0 \\ \\ 2x-4y+8=0 \end{cases} $$
Nota. Las ecuaciones se clasifican como lineales cuando el grado más alto de sus incógnitas es 1.
Vamos a reformular el sistema de ecuaciones en la forma estándar ax+by=c.
Trasladamos los términos constantes al lado derecho de la ecuación, manteniendo las incógnitas y sus coeficientes al lado izquierdo.
$$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$
El siguiente paso es convertir el sistema de ecuaciones a forma vectorial.
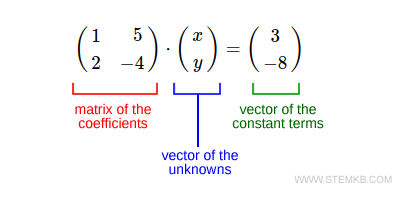
$$ \begin{pmatrix} 1 & 5 \\ 2 & -4 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$
La matriz de la izquierda representa la matriz de coeficientes para las variables incógnitas x y y.
$$ A = \begin{pmatrix} 1 & 5 \\ 2 & -4 \end{pmatrix} $$
El vector en la primera posición es el vector de las incógnitas.
$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} $$
Y el último vector corresponde a los términos constantes de ambas ecuaciones.
$$ \vec{b} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$
Ahora, veamos cómo podemos convertir esta información en variables dentro del entorno de trabajo de Matlab.
Para definir la matriz de coeficientes en Matlab, generamos un arreglo bidimensional.
Introduce A = [1, 5; 2, -4] en la línea de comandos.
>> A = [ 1 , 5 ; 2 , -4 ]
A =
1 5
2 -4
Para definir el vector de términos constantes en Matlab, creamos un arreglo unidimensional.
Escribe b = [3; -8].
>> b = [ 3 ; -8 ]
b =
3
-8
El sistema de ecuaciones en su forma vectorial es el resultado del producto de una matriz por un vector.
$$ A \cdot \vec{x} = \vec{b} $$
Para hallar las soluciones del sistema, despejamos el vector x, trasladando el resto de los términos al lado derecho.
$$ \vec{x} = A^{-1} \cdot \vec{b} $$
El símbolo A-1 representa la matriz inversa de A, que es la matriz de coeficientes del sistema de ecuaciones.
Para calcular A-1·b en Matlab, escribe el comando inv(A)*b.
>> inv(A)*b
ans =
-2
1
Esto nos da los valores de x y y del vector de incógnitas.
$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \end{pmatrix} $$
Con este proceso, hemos encontrado la solución del sistema de ecuaciones.
$$ x=-2 $$
$$ y=1 $$
Así, el sistema de ecuaciones lineales tiene una solución en (x;y)=(-2;1).
Verifica si la solución es correcta. Sustituye los valores x=-2 y y=1 en el sistema de ecuaciones original. A continuación, realiza los cálculos algebraicos. $$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$ $$ \begin{cases} -2 + 5 \cdot 1 =3 \\ \\ 2 \cdot (-2) -4 \cdot 1 =-8 \end{cases} $$ $$ \begin{cases} 3 =3 \\ \\ -8 =-8 \end{cases} $$ Al comprobarse todas las ecuaciones del sistema, confirmamos que la solución x=-2 y y=1 es correcta.