Sustitución de diagonales en matrices con Matlab

En esta lección, les mostraré cómo sustituir elementos en las diagonales de una matriz utilizando Matlab, una herramienta esencial para el cálculo matricial.

¿Qué son las diagonales en una matriz? Corresponden a aquellos elementos ubicados de manera transversal, partiendo desde la esquina superior derecha hasta la inferior izquierda, o en sentido contrario. Un ejemplo claro es la diagonal principal de la matriz M, que incluye los elementos 1, 5, 9. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Veamos un ejemplo práctico para ilustrarlo mejor.

Primero, creamos una matriz cuadrada de 3x3 con tres filas y tres columnas:

>> M=[1 2 3 ; 4 5 6 ; 7 8 9]
M =
1 2 3
4 5 6
7 8 9

La diagonal principal de esta matriz está compuesta por los elementos 1, 5, 9.

$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Para reemplazar estos elementos en Matlab, utilizamos spdiags([-1;-5;-9],0,M). Así, cambiamos los elementos de la diagonal principal por -1, -5, -9.

>> spdiags([-1;-5;-9],0,M)
ans =
-1 2 3
4 -5 6
7 8 -9

• El primer parámetro es el vector columna [-1;-5;-9], que contiene los nuevos valores para la diagonal.
• El segundo parámetro (0) indica el índice de la diagonal a modificar. Recordemos que la diagonal principal tiene índice 0.

  Nota: El índice 1 corresponde a la diagonal superior a la principal, mientras que el -1 a la inferior. Los índices 2 y -2 se refieren a las diagonales aún más alejadas.

• El tercer parámetro, M, es el nombre de la variable donde se almacena la matriz.

Con este comando, hemos modificado la matriz cuadrada, reemplazando los elementos en su diagonal principal.

$$ M = \begin{pmatrix} \color{red}{-1} & 2 & 3 \\ 4 & \color{red}{-5} & 6 \\ 7 & 8 & \color{red}{-9} \end{pmatrix} $$

Ahora, para alterar los elementos en la diagonal superior a la principal, utilizamos spdiags([-1;-5;-9],1,M).

>> spdiags([-1;-5;-9],1,M)
ans =
1 -5 3
4 5 -9
7 8 9

Este comando reemplaza los elementos situados justo por encima de la diagonal principal.

$$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ 4 & 5 & \color{red}{-9} \\ 7 & 8 & 9 \end{pmatrix} $$

Nota: El primer elemento, -1, del vector [-1;-5;-9] no se incluye en la matriz resultante, ya que se encuentra fuera de los límites de esta. Por tanto, solo -5 y -9 son visibles en la matriz.

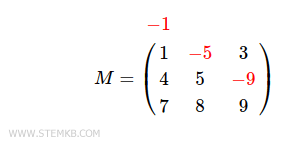
¿Y cómo modificamos los elementos en la diagonal secundaria?

La diagonal secundaria se extiende desde la esquina superior derecha hasta la inferior izquierda.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{3} \\ 4 & \color{red}{5} & 6 \\ \color{red}{7} & 8 & 9 \end{pmatrix} $$

Para cambiar los elementos en la diagonal secundaria, combinamos las funciones spdiags() y fliplr().

>> fliplr(spdiags([-1;-5;-9],0,fliplr(M)))
ans =
1 2 -1
4 -5 6
-9 8 9

La función fliplr() invierte la matriz horizontalmente.

$$ \text{ fliplr }(M) = \begin{pmatrix} 3 & 2 & 1 \\ 6 & 5 & 4 \\ 9 & 8 & 7 \end{pmatrix} $$

Después, spdiags() sustituye los valores en la diagonal principal de la matriz invertida.

$$ \text{ fliplr }(M) = \begin{pmatrix} \color{red}{-1} & 2 & 1 \\ 6 & \color{red}{-5} & 4 \\ 9 & 8 & \color{red}{-9} \end{pmatrix} $$

De este modo, hemos reemplazado los elementos en la diagonal secundaria de la matriz original M.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{-1} \\ 4 & \color{red}{-5} & 6 \\ \color{red}{-9} & 8 & 9 \end{pmatrix} $$

Así, también es posible modificar los valores en las demás diagonales de la matriz.

Nota: Para cambiar las diagonales adyacentes a la secundaria, ajusta el índice en la función spdiags() a 1 o -1. Por ejemplo, para alterar los elementos sobre la diagonal secundaria, utiliza el comando
fliplr(spdiags([-1;-5;-9],1,fliplr(M))) $$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ \color{red}{-9} & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$ De manera inversa, para modificar los elementos bajo la diagonal secundaria, usa el comando
fliplr(spdiags([-1;-5;-9],-1,fliplr(M))) $$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & \color{red}{-1} \\ 7 & \color{red}{-5} & 9 \end{pmatrix} $$