Transposición de matrices en Matlab
En esta sesión, abordaremos el proceso de transposición de matrices utilizando Matlab, detallando cada paso para garantizar una comprensión completa.
Transponer una matriz significa intercambiar sus filas por columnas y viceversa. Como ejemplo, observemos la siguiente matriz:
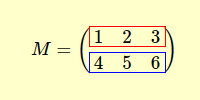
La transpuesta se obtiene reasignando los elementos de cada fila a una columna, y al contrario.
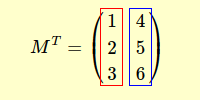
Para ilustrarlo mejor, veamos un ejemplo concreto.
Generemos una matriz rectangular 2x3:
>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6
Esta matriz consta de dos filas y tres columnas, como se muestra a continuación:
$$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} $$
Para transponer la matriz, agregamos un apóstrofo tras el nombre de la variable, de esta manera:
Escribimos M' para obtener la transpuesta:
>> M'
ans =
1 4
2 5
3 6
Además, podemos usar la función transpose(M) para lograr un resultado idéntico.
>> transpose(M)
ans =
1 4
2 5
3 6
Tanto con el apóstrofo como con la función, el resultado es una matriz MT de 3x2, con tres filas y dos columnas:
$$ M^T = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} $$
En conclusión, la transposición de M a MT conlleva la reorganización de las filas en columnas y viceversa, una operación esencial en el ámbito del análisis de matrices.