Matrices dispersas en Matlab

En esta lección en línea, les enseñaré cómo crear matrices dispersas usando Matlab.

¿Qué es una matriz dispersa? Las matrices dispersas permiten generar matrices muy grandes ocupando menos memoria del ordenador. Por ejemplo, al crear una matriz con muchos valores constantes (como cero), se repiten los mismos valores en múltiples elementos, ocupando innecesariamente una gran parte de la memoria. $$ M = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ Para reducir la cantidad de memoria ocupada, puedes generar la misma matriz como una matriz dispersa, donde los datos se comprimen porque se ignoran los valores nulos.

En Matlab, puedes usar matrices dispersas para crear matrices de identidad y diagonales comprimidas.

Matriz de identidad dispersa

Permítanme darles un ejemplo práctico.

Crea una matriz de identidad usando la función eye(4)

>> eye(4)
ans =
Matriz Diagonal
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

Hay 12 ceros y 4 unos en la matriz. Así que, la mayor parte del espacio en la matriz (12 de 16 elementos) está ocupada innecesariamente por ceros.

Ahora crea la misma matriz de identidad usando la técnica de matrices dispersas a través del comando speye(4).

>> speye(4)
ans =
Matriz dispersa de columna comprimida (filas = 4, columnas = 4, nnz = 4 [25%])
(1, 1) -> 1
(2, 2) -> 1
(3, 3) -> 1
(4, 4) -> 1

En la matriz dispersa de Matlab, solo se enumeran las posiciones (fila, columna) de la matriz donde hay valores no nulos, ocupando una menor cantidad de memoria.

Por esta razón, se llama "matriz dispersa".

Tenga en cuenta que la matriz dispersa ocupa menos memoria porque solo considera la información útil. En una matriz de identidad, los ceros son elementos insignificantes en el cálculo de la matriz, por lo que se eliminan. Esto reduce el espacio ocupado en la memoria (complejidad espacial) y reduce el tiempo de ejecución de los cálculos (complejidad temporal).

Puedes usar la matriz dispersa que acabas de crear en cálculos como si fuera una matriz normal.

Por ejemplo, crea una matriz cuadrada M con cuatro filas y cuatro columnas.

>> M=[1 2 3 4;5 6 7 8; 9 0 1 2; 3 4 5 6]
M =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Luego multiplica la matriz M por una matriz de identidad de tamaño 4.

>> M*eye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Ahora multiplica la misma matriz M por una matriz de identidad dispersa de tamaño 4.

>> M*speye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Como puedes ver, el resultado final de las operaciones M*eye(4) y M*speye(4) siempre es el mismo.

Sin embargo, en la operación con la matriz dispersa M*speye(4), obtuviste el resultado más rápido, utilizando una menor cantidad de memoria del ordenador.

Matriz diagonal dispersa

En Matlab, existe una función específica para crear matrices diagonales dispersas. Esta función se llama spdiags().

spdiags(v,i,r,c)

• El primer parámetro (v) es un vector de columna con los elementos que se colocarán en la diagonal
• El segundo parámetro (i) es el índice de la diagonal donde quieres colocar los elementos. Por defecto, es 0 donde cero es la diagonal principal)
• El tercero (r) y cuarto (c) parámetros son el número de filas y columnas de la matriz dispersa a crear

Por ejemplo, escribe spdiags([1;2;3],0,3,3) para crear una matriz diagonal dispersa de tamaño 3x3.

>> spdiags([1;2;3],0,3,3)
ans =
Matriz dispersa de columna comprimida (filas = 3, columnas = 3, nnz = 3 [33%])

(1, 1) -> 1
(2, 2) -> 2
(3, 3) -> 3

Matlab coloca los elementos del vector [1;2;3] en la diagonal principal de una matriz 3x3.

El resultado es una matriz dispersa de la matriz diagonal

$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{pmatrix} $$

Creación manual de matrices dispersas

En Matlab, puedes definir una matriz dispersa detallando la posición de cada valor no cero en la matriz.

Veamos un ejemplo para crear una matriz dispersa a partir de la siguiente matriz:

$$ M = \begin{pmatrix} 3 & 0 & 1 \\ 0 & 1 & 2 \\ 4 & 0 & 0 \end{pmatrix} $$

Primero, anota en un arreglo los valores no cero de la matriz, indicando su fila, columna y valor.

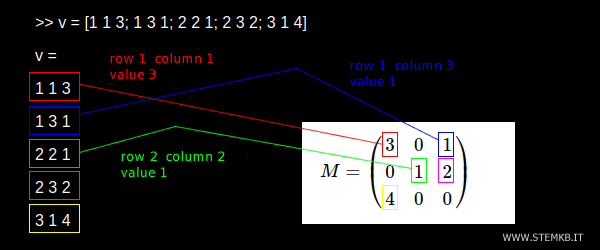
>> v = [1 1 3; 1 3 1; 2 2 1; 2 3 2; 3 1 4]
v =
1 1 3
1 3 1
2 2 1
2 3 2
3 1 4

Cada fila de este arreglo representa la ubicación (fila y columna) y el valor de un elemento no cero en la matriz.

Por ejemplo, el primer elemento no cero (3) se encuentra en la primera fila y columna (1,1), como se muestra en rojo en el ejemplo a continuación. Para representar este elemento en la matriz dispersa, escribe 1 1 3 en una fila del arreglo. Repite este proceso para los demás elementos.

Con el arreglo listo, crea la matriz dispersa utilizando la función spconvert().

>> spconvert(v)

El resultado es una matriz dispersa que refleja los valores y posiciones que has especificado.

ans =
Matriz Dispersa en Columnas Comprimidas (filas = 3, columnas = 3, nnz = 5 [56%])
(1, 1) -> 3
(3, 1) -> 4
(2, 2) -> 1
(1, 3) -> 1
(2, 3) -> 2

Recuerda que puedes definir los elementos no cero de la matriz en cualquier secuencia al crear el arreglo.

Además, es posible indicar la misma posición de la matriz varias veces con distintos valores.

Cabe destacar que si una misma posición en la matriz se define múltiples veces en el arreglo, Matlab sumará todos los valores. Por ejemplo, al indicar los valores 2 y 3 en la posición (1,1), Matlab considerará la suma de estos como 2+3=5 para dicha posición en la matriz.

Este método también facilita la generación de matrices dispersas con números complejos.