Extracción de la diagonal en una matriz con Matlab
En esta lección exploraremos cómo extraer los elementos de la diagonal de una matriz utilizando Matlab.
¿Qué es la diagonal de una matriz? La diagonal principal de una matriz comprende aquellos elementos que se encuentran en la diagonal que va desde el elemento superior izquierdo hasta el inferior derecho. Por ejemplo, en la siguiente matriz, los elementos 1, 5 y 9, resaltados en rojo, conforman la diagonal principal. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$
A continuación, un ejemplo práctico:
Creamos una matriz cuadrada de 3x3, con tres filas y tres columnas, que contenga los siguientes elementos.
>> M=[1 2 3; 4 5 6; 7 8 9]
M =
1 2 3
4 5 6
7 8 9
Para extraer los elementos de la diagonal principal, utilizamos la función diag(M).
>> diag(M)
ans =
1
5
9
Esta función nos permite obtener los elementos situados en la diagonal principal de la matriz, que en este caso son 1, 5 y 9.
$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$
Además, la función diag() puede ser utilizada para acceder a otras diagonales de la matriz.
Por ejemplo, al teclear diag(M,1), se extraen los elementos de la diagonal que se encuentra justo por encima de la diagonal principal.
>> diag(M,1)
ans =
2
6
En este caso, diag(M,1) nos revela los números 2 y 6, ubicados en la diagonal superior a la principal.
$$ M = \begin{pmatrix} 1 & \color{red}2 & 3 \\ 4 & 5 & \color{red}6 \\ 7 & 8 & 9 \end{pmatrix} $$
Si deseamos acceder a la diagonal situada aún más arriba, empleamos la función diag(M,2).
>> diag(M,2)
ans = 3
Con este comando, obtenemos los elementos de la diagonal situada dos niveles por encima de la principal. En este caso, solo el número 3.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$
Para extraer diagonales situadas por debajo de la principal, se especifica un entero negativo como segundo parámetro. Por ejemplo, diag(M,-1) nos permite acceder a los elementos de la diagonal inmediatamente inferior a la principal.
>> diag(M,-1)
ans =
4
8
Con diag(M,-1) extraemos los elementos 4 y 8, ubicados bajo la diagonal principal.
$$ M = \begin{pmatrix} 1 & 2 & 3 \\ \color{red}4 & 5 & 6 \\ 7 & \color{red}8 & 9 \end{pmatrix} $$
Si nuestro objetivo es obtener una matriz donde solo se conserven los elementos de la diagonal principal, utilizaremos diag(diag(M)).
>> diag(diag(M))
ans =
Matriz Diagonal
1 0 0
0 5 0
0 0 9
El resultado es una matriz diagonal, donde solo los elementos de la diagonal principal son distintos de cero.
$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 9 \end{pmatrix} $$
¿Y la diagonal secundaria?
La diagonal secundaria, o antidiagonal, se extiende de derecha a izquierda, iniciando en el elemento superior derecho. En nuestra matriz de ejemplo, la diagonal secundaria está formada por los elementos 3, 5 y 7.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$
Para acceder a esta diagonal, utilizamos la función diag(fliplr(M)), que invierte la matriz horizontalmente antes de aplicar diag().
>> diag(fliplr(M))
ans =
3
5
7
De esta forma, diag(fliplr(M)) nos proporciona los elementos 3, 5 y 7, pertenecientes a la diagonal secundaria.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$
Nota: Esta técnica también permite extraer diagonales situadas por encima o por debajo de la diagonal secundaria. Para acceder a las diagonales superiores, se introduce un número positivo como segundo parámetro. Por ejemplo, diag(fliplr(M),1) extraerá los elementos 2 y 4. $$ M = \begin{pmatrix} 1 & \color{red}2 & \color{green}3 \\ \color{red}4 & \color{green}5 & 6 \\ \color{green}7 & 8 & 9 \end{pmatrix} $$De manera similar, para diagonales inferiores, se utiliza un entero negativo, como en diag(fliplr(M),-1), que seleccionará los elementos 6 y 8. $$ M = \begin{pmatrix} 1 & 2 & \color{green}3 \\ 4 & \color{green}5 & \color{red}6 \\ \color{green}7 & \color{red}8 & 9 \end{pmatrix} $$ .
La función diag() facilita la extracción de elementos diagonales, incluso de matrices rectangulares.
Imagina que generas una matriz rectangular de 3x4, con 3 filas y 4 columnas.
>> M2=[1 1 1 1 ; 2 2 2 2 ; 3 3 3 3]
M2 =
1 1 1 1
2 2 2 2
3 3 3 3
Posteriormente, al ejecutar el comando diag(M2), observarás lo siguiente:
>> diag(M2)
ans =
1
2
3
Este comando, diag(M2), se encarga de seleccionar los elementos que forman la diagonal principal, de izquierda a derecha y comenzando desde el elemento superior izquierdo.
$$ M = \begin{pmatrix} \color{red}1 & 1 & 1 & 1 \\ 2 & \color{red}2 & 2 & 2 \\ 3 & 3 & \color{red}3 & 3 \end{pmatrix} $$
Así, es posible extraer cualquier diagonal, independientemente de si la matriz es cuadrada o no.
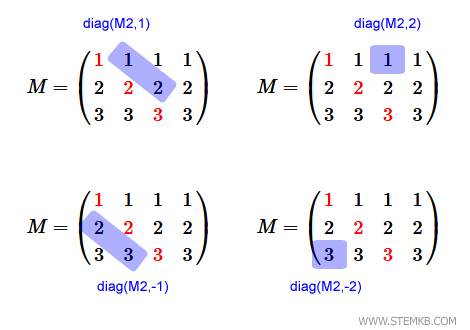
Nota: Para matrices rectangulares, también es viable extraer las diagonales superiores o inferiores a la principal. Esto se logra especificando un entero positivo o negativo como segundo parámetro. Por ejemplo, emplea diag(M2,1) o diag(M2,-1) para acceder a las diagonales superior e inferior a la principal, respectivamente. De manera similar, con diag(M2,2) o diag(M2,-2) podrás enfocarte en las diagonales aún más alejadas.
Para las diagonales secundarias en matrices rectangulares, es necesario invertir la matriz de derecha a izquierda. Por ejemplo, al escribir diag(fliplr(M2)), se extrae la diagonal secundaria, que inicia en el elemento más superior y derecho de la matriz. $$ M = \begin{pmatrix} 1 & 1 & 1 & \color{red}1 \\ 2 & 2 & \color{red}2 & 2 \\ 3 & \color{red}3 & 3 & 3 \end{pmatrix} $$