Vectores en Matlab

En esta clase, exploraremos cómo crear vectores en Matlab.

Empecemos con un ejemplo concreto.

Imagina un vector en el plano que parte del origen (0;0) y se extiende hasta las coordenadas v(2;4).

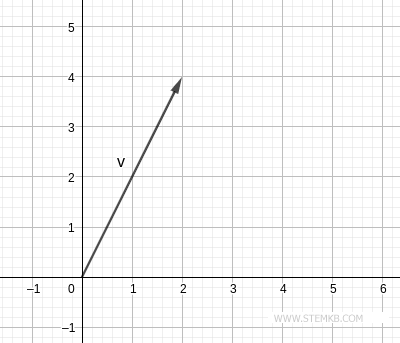
Este vector se compone de dos elementos: x=2 e y=4.

Para representar este vector en Matlab, es necesario emplear una variable de tipo array bidimensional.

En este array, las componentes x e y del vector se separan mediante un punto y coma.

>> v=[2;4]

De esta manera, definimos lo que conocemos como un vector columna.

$$ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

Este array recién creado puede utilizarse en diversas operaciones de cálculo vectorial, como la suma de vectores, el producto cruz y el producto punto.

Creación de un Vector Tridimensional en Matlab

Para formar un vector con tres o más componentes, el procedimiento es similar.

Consideremos, por ejemplo, un vector tridimensional en el espacio 3D que se orienta hacia las coordenadas v(2;4;3).

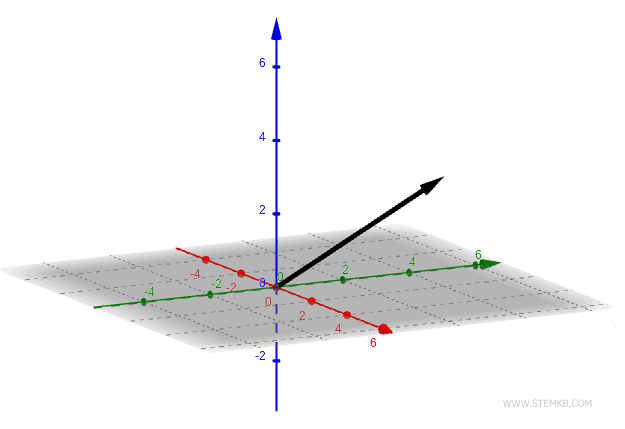
Este vector está formado por tres elementos: x=2, y=4, z=3.

$$ \vec{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ 3 \end{pmatrix} $$

Para definir este vector en Matlab, creamos un array con tres componentes.

>> v=[2;4;3]

Cómo Crear un Vector Fila

Hasta ahora, hemos visto cómo crear vectores columna, donde los elementos se disponen de manera vertical.

$$ \vec{v} = \begin{pmatrix} a \\ b \\ c \end{pmatrix} $$

Si lo que necesitas es un vector fila, con elementos alineados horizontalmente, la sintaxis varía ligeramente.

$$ \vec{v} = \begin{pmatrix} a & b & c \end{pmatrix} $$

Para formar un vector fila en Matlab, se crea un array separando los componentes con espacios o comas.

Por ejemplo, para definir el siguiente vector fila:

$$ \vec{v} = \begin{pmatrix} 1 & 2 & 3 \end{pmatrix} $$

Introducimos un array y separamos los elementos mediante comas.

>> v=[1, 2, 3]

Así obtenemos un vector fila.

Nota: Otra opción es crear primero un vector columna v=[1;2;3] y luego convertirlo en vector fila mediante la transposición de v.