Cómo encontrar la longitud de un vector en Octave

¿Alguna vez te has preguntado cómo determinar la longitud de un vector en Octave? Aquí vamos a despejar esa duda.

La longitud de un vector, ¿qué es? Se trata de la distancia euclídea del vector, a la que también nos referimos como norma. Imagina que un vector es como una flecha; su norma euclídea no es más que la longitud de esa flecha.

Vamos a aterrizarlo con un ejemplo práctico.

Primero, definamos un vector en la variable V:

>> V=[3 4]
V =
3 4

Este es un vector que señala al punto (3;4).

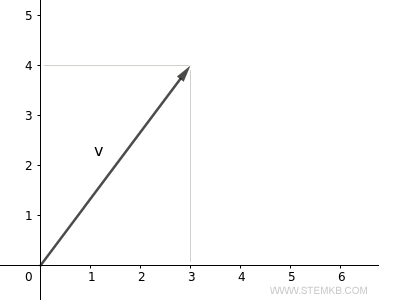
Ahora, para hallar la longitud de este vector (o su magnitud, o norma), simplemente usamos la función norm(V)

>> norm(V)
ans = 5

Por lo tanto, la longitud de nuestro vector (la norma) es igual a 5.

En términos más gráficos, es como si la longitud de nuestra flecha en el plano cartesiano fuera 5.

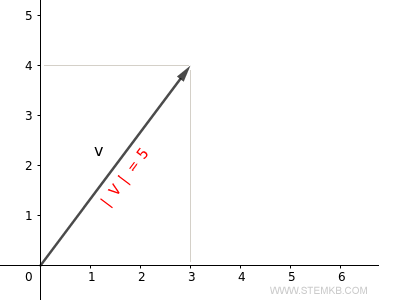
¿Dudas? Veamos si es correcto. La longitud de un vector (o su módulo) puede ser calculada con el teorema de Pitágoras $$ | \vec{v} | = \sqrt{3^2+4^2} = \sqrt{25} = 5 $$ Así que, efectivamente, la longitud de nuestro vector es 5. ¡El resultado está confirmado!