Creación de gráficos polares en Matlab

En esta sesión, profundizaremos en la creación de gráficos polares utilizando Matlab.

¿Qué son los gráficos polares? Estos gráficos, característicos por su forma circular, utilizan coordenadas polares para representar datos. Son ampliamente reconocidos y valorados por su elegancia en el ámbito científico.

Ilustraré este concepto con un ejemplo práctico.

Para comenzar, creamos un arreglo denominado 'theta', que almacenará nuestras variaciones angulares:

>> theta = 0 : 0.1 : 2*pi;

Este comando forma un arreglo que oscila de 0 a 2π (equivalente a 360°) en incrementos de 0.1.

A continuación, definimos otro arreglo, 'y1', asignando valores de la función y1 para cada variación angular en theta:

>> y1=0.5+(1.3).^(theta);

En este punto, 'y1' se convierte en el codominio de nuestra función, mientras 'theta' representa el dominio.

Así, los arreglos theta y y1 mantienen una correspondencia uno a uno en sus elementos.

Con estos arreglos ya preparados, avanzamos hacia la fase más estimulante: la construcción del gráfico polar. Simplemente ingresamos la función Polar() de la siguiente manera:

>> PolarGraph = polar(theta,y1,"*");

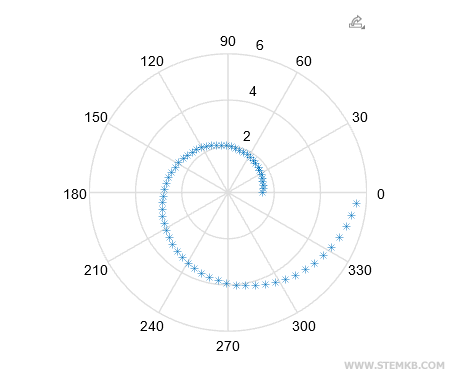
¡Y listo! Matlab nos presentará de manera elegante el comportamiento de la función y1 a través de sus coordenadas polares.

En nuestro caso, logramos generar una impresionante función en forma de espiral.

Pero aún hay más. ¿Y si queremos visualizar dos funciones distintas en un mismo gráfico polar?

Limpiamos la pantalla con 'clf' para reiniciar y volvemos a generar el arreglo 'theta' con las mismas variaciones angulares.

clf

Recreamos el arreglo theta con las variaciones angulares (dominio de la función):

>> theta = 0 : 0.1 : 2*pi;

Ahora, definimos dos nuevos arreglos, 'y1' y 'y2', correspondiendo a dos funciones diferentes que cambian con theta:

>> y1=0.5+(1.3).^(theta);
>> y2 = 3*(1 - cos(theta));

Integramos ambas funciones en una matriz [m]

>> m = [y1;y2];

Finalmente, empleamos la función Polarplot() para elaborar el gráfico polar:

>> PolarGraph = polarplot(theta,m);

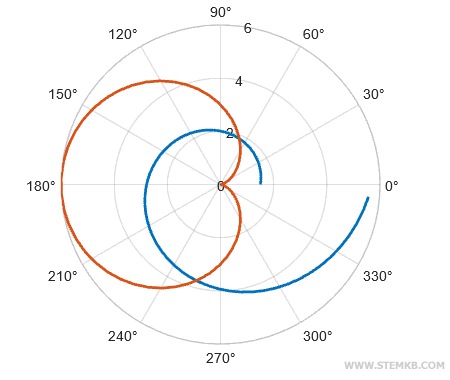
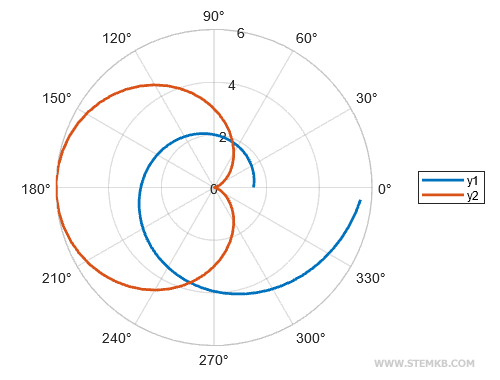
De esta manera, ambas funciones se representan en un único gráfico polar.

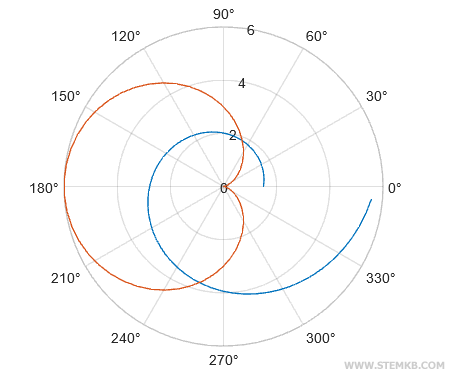
Para aumentar la visibilidad de las líneas del gráfico, podemos ajustar su grosor con la función set().

set(PolarGraph,"LineWidth",2);

Con esto, conseguimos duplicar el espesor de las líneas.

Para añadir un toque final a nuestra obra, incluyamos una leyenda utilizando la función legend().

legend("y1","y2");

La leyenda complementa de manera distinguida el borde de nuestro gráfico.

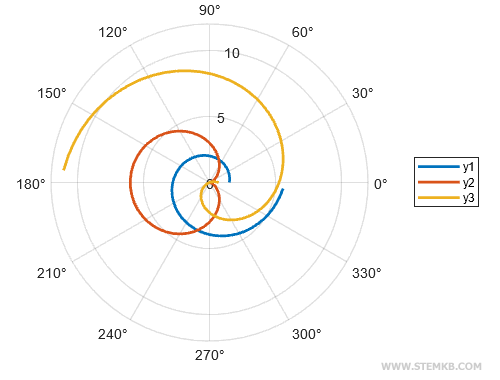
Recuerden, esta técnica no se limita a representar únicamente dos funciones. Podemos visualizar tres o más funciones en un mismo gráfico polar siguiendo el mismo proceso. Definimos funciones adicionales, creamos una matriz con todas ellas, y utilizamos la función polarplot(theta, m) para exponer los gráficos superpuestos. El resultado es un gráfico polar cautivador con múltiples funciones, cada una aportando un atractivo único. Por ejemplo, agregamos una función y3 = 0.7 - (1.9).*theta además de y1 y y2. Luego, creamos una matriz con las tres funciones m = [y1; y2; y3]. Finalmente, empleamos la función polarplot(theta, m) para visualizar los tres gráficos superpuestos en el mismo gráfico polar. Así, el gráfico polar muestra una interesante interacción entre tres funciones distintas.

Ahora, el gráfico polar ilustra las tres funciones.