Variables simbólicas en Matlab

En esta ocasión, abordaremos el tema de las variables simbólicas en Matlab.

¿A qué nos referimos cuando hablamos de una variable simbólica? Esencialmente, se trata de un tipo particular de variable que almacena exclusivamente el símbolo, tal como "x", destinado a cálculos. No conserva un valor numérico concreto. Esta característica nos habilita para realizar operaciones algebraicas simbólicas con una o múltiples incógnitas, como solucionar ecuaciones con dos o más variables o efectuar la suma de polinomios.

La función syms es la herramienta que utilizamos para definir una variable simbólica.

A modo de ilustración, si deseamos definir una variable simbólica "x", procedemos de la siguiente manera:

>> syms x

Asimismo, es factible definir múltiples variables simbólicas simultáneamente, enumerándolas consecutivamente y separándolas por espacios:

>> syms x y

Cada vez que se define una variable simbólica, esta es visible en el entorno de trabajo de Matlab.

Estas variables están vinculadas a la clase "sym".

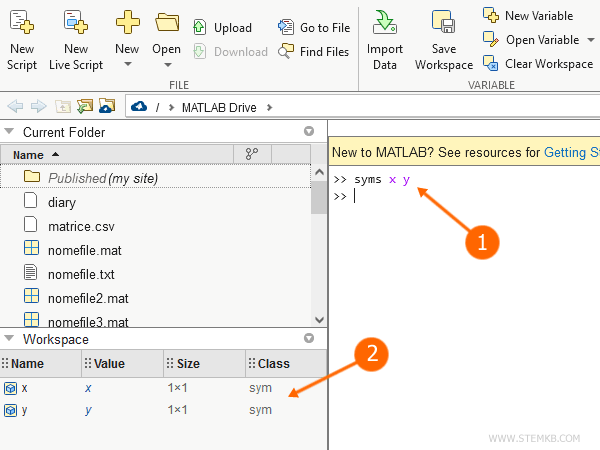
A continuación, expondremos un ejemplo práctico.

Supongamos que manejamos dos polinomios:

$$ P(x) = 2x + y $$

$$ Q(x) = 4x - 2y $$

Y nuestro objetivo es multiplicarlos:

$$ P(x) \cdot Q(x) = (2x + y) \cdot (4x - 2y) $$

Para ejecutar este cálculo algebraico en Matlab, primero definimos las variables simbólicas "x" y "y" mediante el comando "syms x y":

>> syms x y

Posteriormente, ingresamos la expresión pq = (2x+y)(4x-2y):

>> pq = (2*x+y)*(4*x-2*y)

ans =
(4*x - 2*y)*(2*x + y)

Matlab identifica a "x" y "y" como elementos simbólicos y configura la expresión correspondiente.

En este contexto, Matlab no reemplaza "x" y "y" por cifras numéricas, sino que los integra como representantes de variables no definidas

Para concretar el cálculo algebraico, recurrimos a la función expand(pq).

>> expand(pq)

ans =
8*x^2 - 2*y^2

Matlab lleva a cabo la operación algebraica simbólica, entregando como resultado el producto de los polinomios en cuestión.

Dicho resultado se expresa como 8x²-2y²

Para validar la exactitud del resultado, multiplicamos algebraicamente ambos polinomios: $$ P(x) \cdot Q(x) = (2x + y) \cdot (4x - 2y) $$ $$ P(x) \cdot Q(x) =2x \cdot 4x + 2x \cdot (-2y) + y \cdot 4x + y \cdot (-2y) $$ $$ P(x) \cdot Q(x) =8x^2 - 4xy + 4xy -2y^2 $$ $$ P(x) \cdot Q(x) =8x^2 -2y^2 $$ Como se puede observar, el resultado es coherente. Esto concluye nuestra exposición de hoy.