Límites de funciones con Matlab
Hoy nos sumergiremos en el apasionante universo de los límites de funciones, aprovechando al máximo las herramientas computacionales que Matlab nos ofrece. No solo desentrañaremos la esencia de este concepto, sino que también lo aplicaremos mediante ejemplos clarificadores.
Antes de adentrarnos, es esencial entender qué son los límites de funciones. Básicamente, un límite muestra el valor al que tiende una función cuando su variable independiente se acerca a un punto específico. Dicho de forma sencilla, nos da una visión del comportamiento de la función en las cercanías de ese punto.
Comenzamos introduciendo 'x', nuestra variable independiente, en la línea de comandos de Matlab con el comando 'syms'
syms x
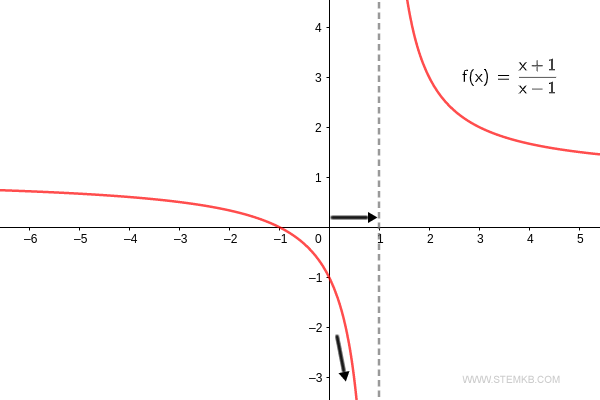
Prosigamos con la función f(x) = (x+1)/(x-1), teniendo a 'x' como nuestra variable protagonista. Nuestro objetivo es determinar el límite cuando 'x' tiende al infinito.
$$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} $$
A continuación, emplearemos el comando 'limit()'. Ingresamos f(x) como primer parámetro, 'x' como segundo y 'Inf' (para indicar infinito positivo) como tercero. Tras ello, presionamos enter.
limit((x+1)/(x-1),x,Inf)
Con precisión, Matlab nos arroja el resultado.
ans = (sym) 1
Así, observamos que el límite de nuestra función al acercarse al infinito es, inequívocamente, uno.
Pero no me creas solo a mí. Como podemos observar, el límite de la función f(x) = (x+1)/(x-1) cuando 'x' se acerca a infinito es, efectivamente, uno. $$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} = 1 $$ El límite de nuestra función es uno cuando 'x' se dirige hacia infinito. El límite de la función cuando x tiende a infinito es 1.
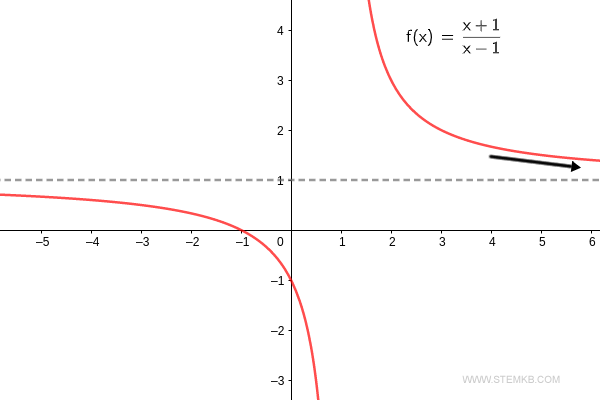
Si te intriga saber qué ocurre cuando x tiende a -∞, añade '-inf' como tercer parámetro:
limit((x+1)/(x-1),x,-inf)
Al hacer 'x' una zambullida hacia el infinito negativo, curiosamente, la función se eleva nuevamente a uno.
ans = (sym) 1
Para respaldar lo dicho, el límite de la función f(x) = (x+1)/(x-1) cuando x tiende a -∞ es un sólido uno. $$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = 1 $$ Puedes observar la gráfica de la función mientras se extiende hacia el infinito negativo. 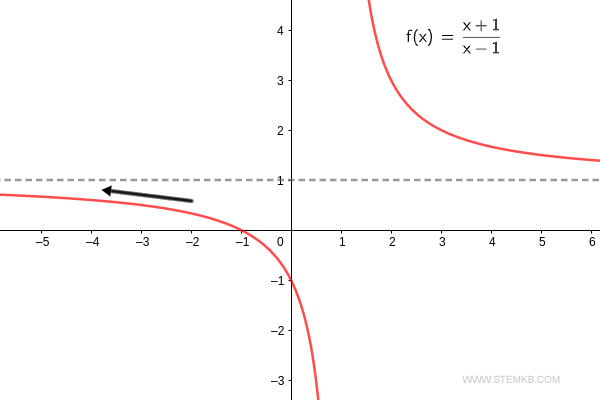
Si tu interés recae en un punto de acumulación específico, como 'x0', simplemente indica ese punto como tercer parámetro.
Por ejemplo, busquemos el límite de la función cuando 'x' tiende a dos:
limit((x+1)/(x-1),x,2)
En este caso, el límite es tres.
ans = (sym) 3
Para verificar, el límite de la función f(x) = (x+1)/(x-1) cuando x tiende a 2 es tres. $$ \lim_{x \rightarrow 2} \frac{x+1}{x-1} = 3 $$ Así, el límite de la función es 3 cuando 'x' se desplaza hacia 2.
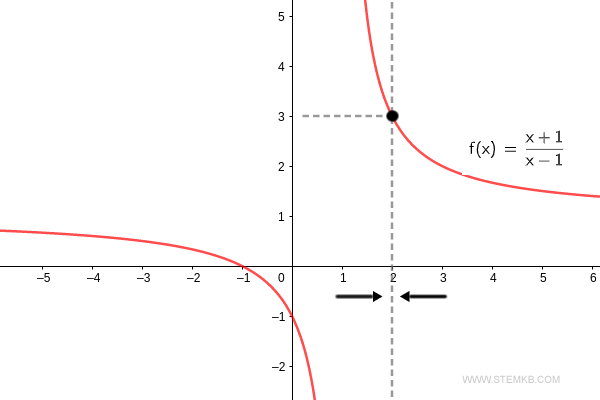
Si lo que buscas es el límite por la derecha, añade 'right' como cuarto argumento.
limit((x+1)/(x-1),x,1,'right')
El resultado indica que el límite por la derecha, al acercarse 'x' a 1, es infinito positivo (∞).
ans = (sym) ∞
Para confirmarlo, cuando la función f(x) = (x+1)/(x-1) se acerca a x=1+ desde la derecha, se dispara hacia el infinito positivo. $$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} = + \infty $$ Así, el límite por la derecha de la función se eleva al infinito cuando 'x' converge en uno.
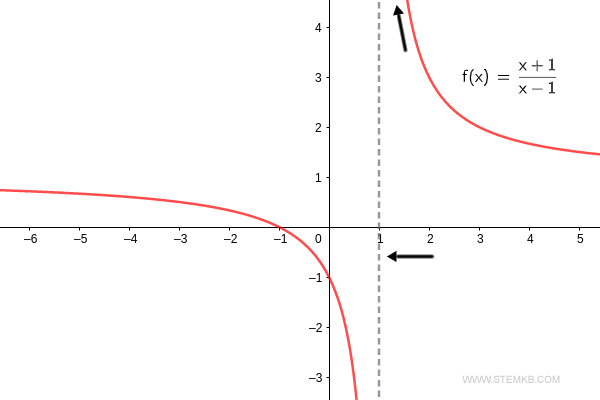
Por otro lado, si deseas conocer el límite por la izquierda, utiliza 'left' como cuarto parámetro.
limit((x+1)/(x-1),x,1,'left')
El hallazgo es que, al acercarse 'x' a 1 por la izquierda, el valor se desploma al infinito negativo (-∞).
ans = (sym) -∞
Al revisar, vemos que el límite por la izquierda de la función f(x) = (x+1)/(x-1) cuando x tiende a 1- es, de hecho, el infinito negativo. $$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = - \infty $$ Y así es, el límite por la izquierda de la función cae al infinito negativo cuando 'x' se acerca a uno.
Con estos conocimientos, estás más que capacitado para explorar y calcular límites de funciones en Matlab con soltura y precisión.