La función polyfit() en Matlab
Hoy te presentaré una función sumamente útil en Matlab conocida como polyfit(). Esta herramienta es ideal para encontrar un polinomio que se ajuste a una serie de datos.
polyfit(Y)
El parámetro principal de esta función es un arreglo que contiene los datos a analizar.
Veamos un ejemplo práctico con el siguiente conjunto de datos:
>> X = [ 1 2 3 4 5 6 ]
>> Y = [ 3 8 6 9 7 8 ]
Para visualizar estos datos, utilizaremos la función plot(X,Y), que nos permite crear un gráfico representativo.
>> plot(X,Y)
El gráfico resultante se verá así:
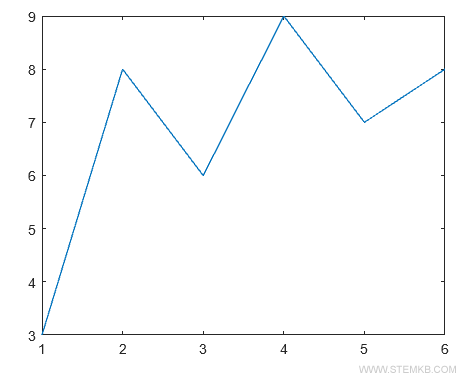
Ahora, si nuestro objetivo es hallar un polinomio de primer grado que se ajuste a estos datos, aplicaremos la función polyfit(X,Y,1). Esta nos proporcionará los coeficientes del polinomio deseado.
>> P = polyfit(X,Y,1)
Los coeficientes obtenidos serán:
P =
0.71429 4.33333
Estos valores corresponden a los coeficientes del polinomio de primer grado, expresado como:
$$ P_1(x) = 0.71429 \cdot x + 4.33333 $$
Para calcular los valores del polinomio en cada punto del arreglo X, usamos la función polyval(), introduciendo los coeficientes del polinomio y el arreglo X.
>> polyval(P,X)
El resultado será:
ans =
5.0476 5.7619 6.4762 7.1905 7.9048 8.6190
Finalmente, para una visualización completa, mostramos tanto los datos originales como el ajuste polinomial en un plano cartesiano con la función plot().
plot(X,Y,X,polyval(P,X))
De esta manera, el polinomio de primer grado traza una línea que aproxima la serie de datos.
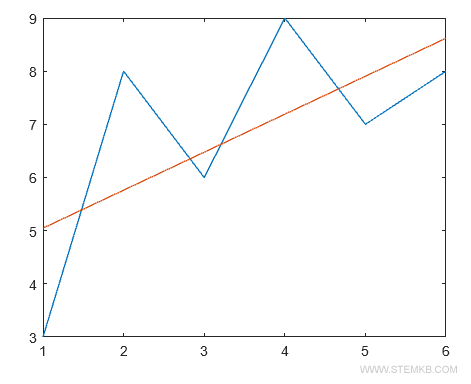
Ejemplo 2
Supongamos ahora que queremos ajustar un polinomio de segundo grado a los mismos datos. El proceso es similar, cambiando el argumento de 1 a 2 en la función polyfit().
>> P = polyfit(X,Y,2)
Obtendremos los coeficientes del polinomio de segundo grado, que luego aplicaremos en la función polyval() para calcular los valores del polinomio en cada punto de X.
P =
-0.35714 3.21429 1.00000
Los coeficientes del polinomio de segundo grado son:
$$ P_2(x) = -0.35714 \cdot x^2 + 3.21429 x + 1.0 $$
Utilizando polyval(P,X), calculamos los valores del polinomio:
>> polyval(P,X)
Y obtenemos el siguiente arreglo de resultados:
ans =
3.8571 6.0000 7.4286 8.1429 8.1429 7.4286
Con la función plot(), mostramos tanto los datos como el ajuste polinomial en un gráfico.
plot(X,Y,X,polyval(P,X))
El polinomio de segundo grado (línea roja) se ajusta a la serie de datos de manera más precisa.
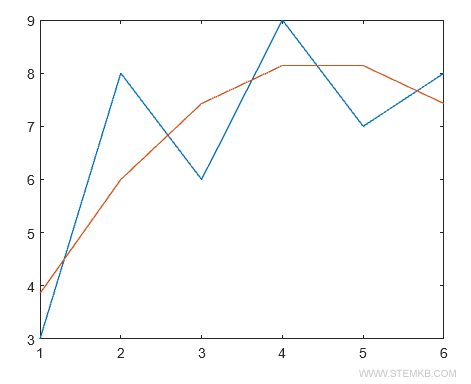
Ejemplo 3
Para concluir, repitamos el proceso con un polinomio de tercer grado. La metodología es la misma, solo cambia el grado del polinomio en la función polyfit().
>> P = polyfit(X,Y,3)
Los coeficientes resultantes son:
P =
0.18519 -2.30159 9.08466 -3.66667
Correspondientes al polinomio de tercer grado:
$$ P_3(x) = 0.18519x^3 -2.30159 \cdot x^2 + 9.08466 x - 3.66667 $$
Aplicando polyval(P,X), obtenemos los valores del polinomio:
>> polyval(P,X)
Y el resultado es:
ans =
3.3016 6.7778 7.8730 7.6984 7.3651 7.9841
Finalmente, visualizamos los datos y el ajuste polinomial en un gráfico con plot().
plot(X,Y,X,polyval(P,X))
El polinomio de tercer grado (línea roja) ofrece una aproximación aún más precisa a la serie de datos.
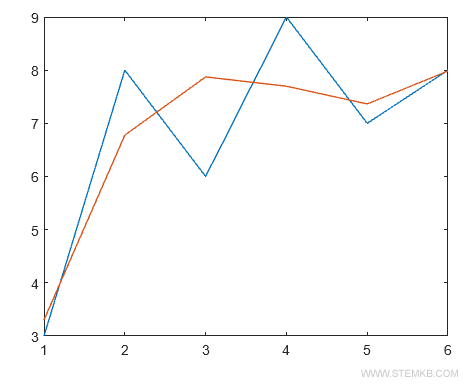
Así, al incrementar el grado del polinomio, se reduce el error de aproximación, logrando un ajuste más preciso a la serie de datos. Esto demuestra la eficacia de polyfit como herramienta