Integrales Definidas en Matlab

Hoy, te llevaré de la mano a través del fascinante mundo de las integrales definidas en Matlab.

¿Te has preguntado alguna vez qué es una integral definida? Básicamente, nos permite determinar el área entre una función f(x), conocida como función integrando, y el eje x en un intervalo concreto (a, b). Esta se representa con la notación $$ \int_a^b f(x) \ dx $$

Para adentrarnos en las integrales definidas en Matlab, contamos con dos herramientas esenciales. Empezaremos con la función int().

La función int()

Para hallar la integral definida de una función en Matlab, simplemente utilizamos la función int().

int(función, a, b)

Esta función tiene una estructura sencilla de tres parámetros:

• El primero define la expresión de la función integrando, f(x).
• El segundo establece el límite inferior de integración, a.
• El tercero, en cambio, determina el límite superior de integración, b.

La función int() opera con cálculos simbólicos. Por ello, antes de introducir la expresión de la función integrando, es imprescindible definir la variable como un símbolo usando la función syms.

Ilustremos esto con un ejemplo práctico.

Tomemos, por ejemplo, la integral elemental:

$$ \int_1^2 2x \ dx $$

Aquí, la función integrando es f(x)=2x, y el intervalo de integración es (1,2).

Primero, es necesario definir x como símbolo a través de syms.

syms x

A continuación, empleamos el comando int(), tomando la expresión 2*x como parámetro principal.

Introduce 1 como límite inferior y 2 como límite superior para el intervalo de integración (1,2).

int(2*x,1,2)

El resultado nos brinda la integral definida de 2x en el intervalo (1,2).

ans = 3

En este escenario, la integral definida es 3.

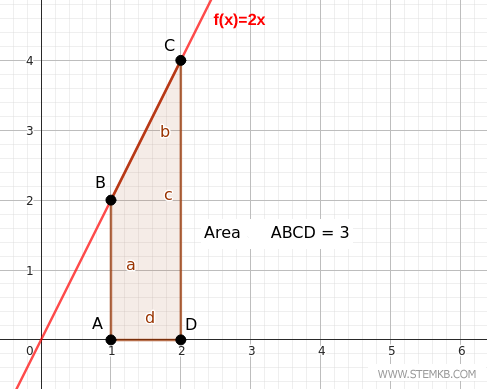
Para verificarlo, basta con observar que la integral definida de 2x en el intervalo (1,2) es directa. La antiderivada de f(x)=2x es $$ \int_1^2 2x \ dx = [ x^2]_1^2 = 2^2 - 1^2 = 4 - 1 = 3 $$ Al visualizar la función en un gráfico cartesiano, se aprecia que el resultado de la integral definida ∫12 2x dx representa el área entre el gráfico de la función f(x)=2x y el eje x en el intervalo (1,2).

La función quad()

Ahora, veamos otra herramienta: la función quad().

Para calcular la integral definida de una función, también podemos emplear quad() en Matlab. Su uso es bastante intuitivo.

Simplemente invocamos la función quad(), proporcionando la función integrando y los límites de integración a y b:

quad(función, a, b)

Como ejemplo, retomemos la integral previamente mencionada, de 1 a 2 de 2x dx.

$$ \int_1^2 2x \ dx $$

La función integrando es f(x)=2x, y el intervalo de integración es (1,2).

Para evaluarla, creamos una función anónima f = @(x) 2*x

>> f = @(x) 2*x

Posteriormente, empleamos quad(f,1,2) para obtener la integral definida del intervalo 1 a 2.

>> quad(f,1,2)

La función quad() estima el área bajo la curva de f(x)=2x en el intervalo (1,2), y nos devuelve el resultado: 3.

ans=3

Cabe señalar que este es el mismo resultado obtenido previamente, donde resolvimos la integral de manera analítica con el teorema fundamental del cálculo. $$ \int_1^2 2x \ dx = [ x^2]_1^2 = 2^2 - 1^2 = 4 - 1 = 3 $$

Diferencias entre int y quad

Quizá te preguntes cuál es la diferencia entre int() y quad() en Matlab.

Aunque ambas se utilizan para calcular la integral definida de una función, se basan en metodologías distintas.

• La función int() resuelve integrales definidas utilizando métodos numéricos, como la regla del trapecio.
• Por otro lado, la función quad() emplea un método de cuadratura adaptativa basado en el algoritmo de Gauss-Kronrod, que por lo general requiere menos llamadas a la función que se integra, lo que lo convierte en un método eficiente.

Así que, esto es todo sobre cómo calcular integrales usando Matlab, una herramienta indispensable para ingenieros, físicos y matemáticos.

Con dedicación y práctica, dominarás quad() y otros métodos de integración numérica, resolviendo una amplia variedad de problemas.