Polinomios en Matlab

Exploraremos el concepto de polinomios en Matlab.

¿Qué es un polinomio? Un polinomio no es más que una expresión compuesta por constantes y variables, conocidas como monomios, que tienen exponentes enteros y se combinan mediante operaciones aritméticas fundamentales: suma, resta, multiplicación y división. Tomemos, por ejemplo, este polinomio de cuarto grado: $$ P(x) = x^4 + 2x^3 - x^2 + 4x +1 $$ El mayor exponente de la variable x determina que es un polinomio de grado cuatro.

Definiendo un polinomio en Matlab

Para definir un polinomio en Matlab, usaremos el siguiente ejemplo.

$$ P(x) = x^4 + 2x^3 - x^2 + 4x +1 $$

Este polinomio consta de una sola variable desconocida (x).

En Matlab, representamos un polinomio mediante un vector que contiene los coeficientes de los términos del polinomio.

>> P = [1 2 -1 4 1]

El arreglo P almacena los coeficientes del polinomio P(x)=x⁴+2x³-x²+4x+1, donde:

• El primer elemento corresponde al coeficiente de x⁴, que es 1.
• El segundo elemento es el coeficiente de 2x³, que es 2.
• El tercer elemento, correspondiente a -x², es -1.
• El cuarto elemento es el coeficiente de 4x, que es 4.
• El quinto y último elemento representa el término constante +1.

Con el vector definido, puedes calcular valores del polinomio P(x) variando x mediante la función polyval().

Para determinar el valor de P(x) cuando x=0, usarías: polyval(P,0)

>> polyval(P,0)

Matlab realiza la sustitución de x por cero y proporciona el resultado correspondiente.

En este caso, el resultado es 1.

ans = 1

Comprobación: Puedes verificar este resultado sustituyendo x=0 en el polinomio original: $$ P(0) = 0^4 + 2 \cdot 0^3 - 0^2 + 4 \cdot 0 +1 $$ El cálculo confirma que $$ P(0)=1 $$

De la misma forma, puedes evaluar el polinomio en x=1 con polyval(P,1)

>> polyval(P,1)

Obteniendo como resultado 7.

ans = 7

Comprobación: Verifica sustituyendo x=1 en el polinomio: $$ P(1) = 1^4 + 2 \cdot 1^3 - 1^2 + 4 \cdot 1 +1 $$ lo que da como resultado $$ P(1)=7 $$

Si lo desea, también puede calcular el valor del polinomio en un rango de valores de x.

Por ejemplo, escriba x=0:5 para crear un arreglo x con los valores desde 0 hasta 5.

>> x=0:5
x =
0 1 2 3 4 5

Ahora calcule los valores del polinomio en el rango de 0 a 5 utilizando la función polyval(P,x)

>> polyval(P,x)

La función calcula los valores del polinomio para cada elemento del arreglo x.

En este caso, el resultado es un arreglo compuesto por 6 elementos.

ans =
1 7 37 139 385 871

Cada elemento es el valor del polinomio en el intervalo (0,5).

Nota. El primer elemento del arreglo es P(0)=1 cuando x=0. El segundo elemento es P(1)=7 cuando x=1. El tercer elemento es P(2)=37. El cuarto elemento es P(3)=139. Y así sucesivamente.

El uso de arreglos permite realizar cálculos de manera rápida.

Además, también permiten representar gráficamente el polinomio en un plano cartesiano utilizando la función plot().

Por ejemplo, escriba estos comandos en secuencia.

>> x=0:5;
>> P = [1 2 -1 4 1] ;
>> y=polyval(P,x);
>> plot(x,y);

El resultado es la gráfica del polinomio en el intervalo (0,5).

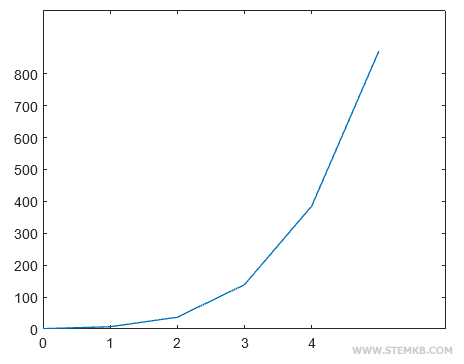
En el eje horizontal se miden los valores de la variable desconocida x, mientras que en el eje vertical los del polinomio y.

Operaciones con polinomios

Puedes utilizar Matlab para realizar operaciones con polinomios.

Déjame darte un ejemplo práctico.

Define el polinomio x³+2x²+3 en el arreglo P1

>> P1 = [ 1 2 0 3 ]

Luego define el polinomio 2x³-x²+3x+1 en el arreglo P2

>> P2 = [ 2 -1 3 1 ]

Ahora realiza estas operaciones:

Adición

Para sumar los dos polinomios, escribe P1+P2

>> P1+P2
ans =
3 1 3 4

El resultado es el polinomio 3x³+x²+3x+4

$$ P_1(x) + P_2(x) = (x^3+2x^2+3) + (2x^3-x^2+3x+1) $$ $$ P_1(x) + P_2(x) = x^3+ 2x^3+2x^2-x^2+3x+1+3 $$ $$ P_1(x) + P_2(x) = 3x^3+x^2+3x+4 $$

Sustracción

Para calcular la diferencia entre los polinomios, escribe P1-P2

>> P1-P2
ans =
-1 3 -3 2

El resultado es el polinomio -x³+3x²-3x+2

$$ P_1(x) - P_2(x) = (x^3+2x^2+3) - (2x^3-x^2+3x+1) $$ $$ P_1(x) - P_2(x) = x^3- 2x^3+2x^2+x^2-3x+1-3 $$ $$ P_1(x) + P_2(x) = -x^3+3x^2-3x+2 $$

Multiplicación

Para calcular el producto entre los polinomios P1·P2, se necesita utilizar la función de convolución conv()

>> conv(P1,P2)
ans =
2 3 1 13 -1 9 3

El resultado es el polinomio 2x⁶+3x⁵+x⁴+13x³-x²+9x+3

$$ P_1(x) \cdot P_2(x) = (x^3+2x^2+3) \cdot (2x^3-x^2+3x+1) $$ $$ P_1(x) \cdot P_2(x) = x^3 \cdot (2x^3-x^2+3x+1) + 2x^2 \cdot (2x^3-x^2+3x+1) + \\ \ \ + 3 \cdot (2x^3-x^2+3x+1) $$ $$ P_1(x) \cdot P_2(x) = 2x^6-x^5+3x^4+x^3 + 4x^5-2x^4+6x^3+2x^2 + \\ \ \ + 6x^3-3x^2+9x+3 $$ $$ P_1(x) \cdot P_2(x) = 2x^6+(4x^5-x^5)+(3x^4-2x^4)+(x^3 +6x^3+ 6x^3) + \\ \ \ + (2x^2-3x^2)+9x+3 $$ $$ P_1(x) \cdot P_2(x) = 2x^6+3x^5+x^4+13x^3 -x^2+9x+3 $$

División

Para calcular el cociente de dos polinomios, necesitas utilizar la función de deconvolución deconv()

>> [q,r] = deconv(P1,P2)
q = 0.50000
r = 0.00000 2.50000 -1.50000 2.50000

La función deconv() devuelve dos resultados:

• el polinomio cociente (q)
• el polinomio resto (r)

El resultado es el polinomio cociente q=0,5

$$ Q = \frac{1}{2} $$

con resto r=2,5x²-1,5x+2,5

$$ R = \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$

Verificación. Realiza cálculos algebraicos para verificar si el producto es correcto. $$ P_1(x) : P_2(x) = \frac{x^3+2x^2+3}{2x^3-x^2+3x+1} $$ En este caso el cálculo es un poco largo.

El polinomio cociente es $$ Q= \frac{1}{2} $$ con resto $$ R = \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ Multiplica el cociente por el polinomio divisor y suma el resto: $$ Q \cdot (2x^3 -x^2+3x+1) + R $$ $$ \frac{1}{2} \cdot (2x^3 -x^2+3x+1) + \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ $$ x^3 - \frac{1}{2} x^2+ \frac{3}{2}x+ \frac{1}{2}+ \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ $$ x^3 + \frac{5-1}{2} x^2+ \frac{3-3}{2}x+ \frac{5+1}{2} $$ $$ x^3 + \frac{4}{2} x^2+ \frac{0}{2}x+ \frac{6}{2} $$ $$ x^3 + 2 x^2+ 3 $$ El resultado es el polinomio dividendo. Por lo tanto, el resultado de la división entre los dos polinomios es correcto.