Límite de una función en Octave

Para aquellos que se adentran en el mundo de Octave y desean calcular límites de funciones, les ofrezco una guía paso a paso con ejemplos prácticos.

Requisitos previos. Es esencial contar con GNU Octave ya instalado en tu ordenador, así como el módulo Symbolic. Si ya lo tienes, podemos comenzar.
Interfaz gráfica de Octave

Una vez dentro, el primer paso es definir la variable independiente x. Para ello, utilizamos el comando syms

syms x

Con esto listo, vamos a calcular el límite de la función f(x)=(x+1)/(x-1) cuando x tiende a infinito:

$$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} $$

Para ello, introducimos el comando limit() de la siguiente manera:

limit((x+1)/(x-1),x)

Octave, con su eficiencia característica, nos devolverá:

ans = (sym) 1

Esto nos indica que, en este caso, el límite de la función es 1.

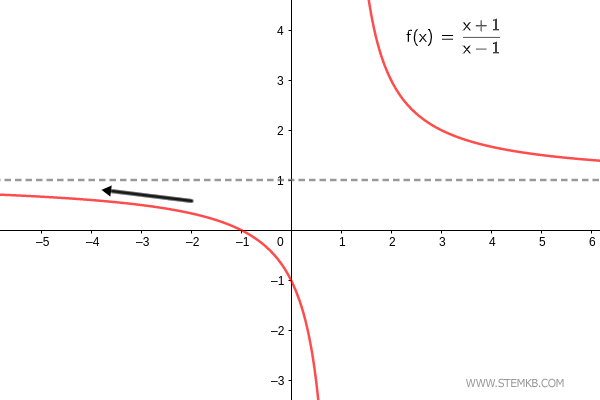
Si analizamos la función f(x)=(x+1)/(x-1) cuando x→∞ confirmamos que el límite es efectivamente 1.. $$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} = 1 $$ La gráfica de la función nos mostrará cómo se comporta f(x) cuando x tiende a infinito.

Si nuestro interés radica en calcular el límite cuando x tiende a menos infinito, el procedimiento es similar:

limit((x+1)/(x-1),x,-inf)

El límite de la función es 1 cuando x→-∞.

ans = (sym) 1

El límite de la función f(x)=(x+1)/(x-1) cuando x→-∞ es 1. $$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = 1 $$
La gráfica de la función

Evaluación de límites en puntos específicos

Para evaluar un límite cuando x tiende a un valor x₀, donde x₀ es un número finito, introduce el mismo comando indicando x₀ en el tercer parámetro.

Supongamos que queremos evaluar el límite de nuestra función cuando x tiende a 2:

limit((x+1)/(x-1),x,2)

El resultado que obtenemos es 3

ans = (sym) 3

Esto significa que el límite de f(x)=(x+1)/(x-1) cuando x→2 es 3. $$ \lim_{x \rightarrow 2} \frac{x+1}{x-1} = 3 $$ 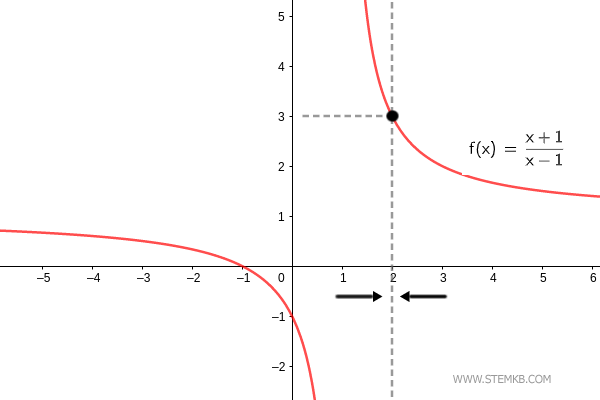La gráfica de la función cuando x tiende a 2

Para límites laterales, Octave también nos ofrece soluciones precisas.

Si solo quieres calcular el límite por la derecha, utiliza el mismo comando y escribe 'right' en el cuarto parámetro.

Por ejemplo, si queremos calcular el límite por la derecha cuando x se aproxima a uno:

limit((x+1)/(x-1),x,1,'right')

El resultado es infinito, representado por ∞

ans = (sym) ∞

El límite de la función f(x)=(x+1)/(x-1) cuando x→1⁺ es infinito. $$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} = + \infty $$ 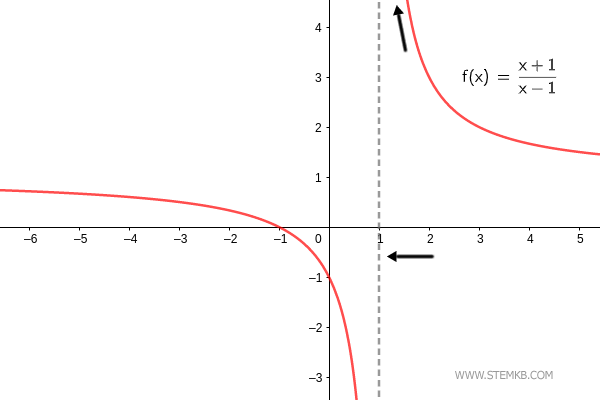La gráfica de la función cuando x tiende a 2 por la derecha

Y, de manera similar, para calcular el límite por la izquierda, utiliza el mismo comando y escribe 'left' en el cuarto parámetro.

limit((x+1)/(x-1),x,1,'left')

El resultado es menos infinito ( -∞ )

ans = (sym) -∞

El límite de la función por la izquierda f(x)=(x+1)/(x-1) cuando x se aproxima a uno (x→1^-) es menos infinito. $$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = - \infty $$ 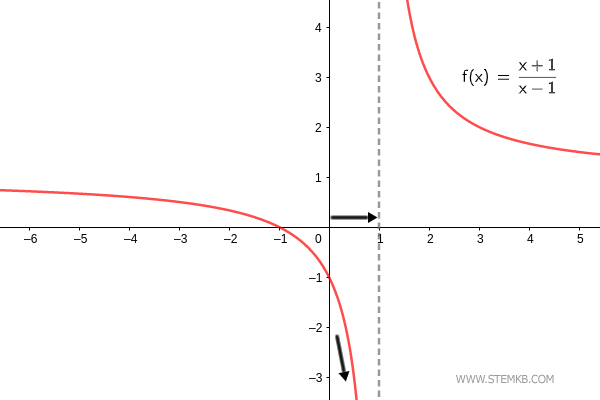El límite por la izquierda de la función cuando x se aproxima a uno.

Espero que esta guía te haya sido de utilidad. En Octave, como en cualquier herramienta, la práctica hace al maestro.

Te invito a seguir explorando y, por supuesto, a continuar acompañándonos en este viaje matemático.