Cómo modificar las diagonales de una matriz en Octave

En esta lección, vamos a aprender a cambiar los elementos de una diagonal en una matriz.

Primero, ¿qué entendemos por diagonales de una matriz? Son los conjuntos de elementos que se extienden desde la esquina superior derecha hasta la esquina inferior izquierda, y viceversa. Por ejemplo, la diagonal principal de la matriz M está formada por los elementos 1, 5, 9. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Veamos un ejemplo práctico.

Generamos una matriz 3x3

>> M=[1 2 3 ; 4 5 6 ; 7 8 9]
M =
1 2 3
4 5 6
7 8 9

La diagonal principal está compuesta por los elementos 1, 5, 9.

$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Si queremos reemplazar los elementos de la diagonal principal con -1, -2, -3, escribimos spdiags([-1;-5;-9],0,M)

>> spdiags([-1;-5;-9],0,M)
ans =
-1 2 3
4 -5 6
7 8 -9

• El primer parámetro es un vector columna [-1;-5;-9] con los nuevos elementos de la diagonal.
• El segundo parámetro (0) es el índice de la diagonal. La diagonal principal tiene índice 0.

  El índice 1 corresponde a la diagonal por encima de la diagonal principal, mientras que el índice -1 corresponde a la diagonal por debajo.

• El tercer parámetro M es la variable donde se almacena la matriz.

El resultado es una matriz cuadrada con los nuevos elementos en la diagonal principal.

$$ M = \begin{pmatrix} \color{red}{-1} & 2 & 3 \\ 4 & \color{red}{-5} & 6 \\ 7 & 8 & \color{red}{-9} \end{pmatrix} $$

Si queremos cambiar los elementos en la diagonal por encima de la diagonal principal, escribimos spdiags([-1;-5;-9],1,M)

>> spdiags([-1;-5;-9],1,M)
ans =
1 -5 3
4 5 -9
7 8 9

La función reemplaza los elementos por encima de la diagonal principal.

$$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ 4 & 5 & \color{red}{-9} \\ 7 & 8 & 9 \end{pmatrix} $$

El primer elemento -1 del vector columna [-1;-5;-9] no aparece en la nueva matriz porque, en este caso, está fuera de la matriz.

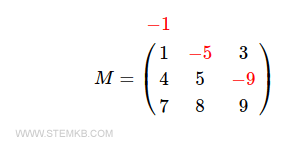
Para reemplazar elementos en la diagonal secundaria, combinamos las funciones spdiags() y fliplr()

>> fliplr(spdiags([-1;-5;-9],0,fliplr(M)))
ans =
1 2 -1
4 -5 6
-9 8 9

Esta función reemplaza los valores en la diagonal secundaria de la matriz.

La diagonal secundaria se extiende desde la esquina superior derecha hasta la esquina inferior izquierda.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{-1} \\ 4 & \color{red}{-5} & 6 \\ \color{red}{-9} & 8 & 9 \end{pmatrix} $$

De esta forma, también puedes modificar todos los valores en las diagonales secundarias de la matriz.