La transposición de una matriz en Octave

Hoy, vamos a abordar un concepto clave en matemáticas: la transposición de una matriz, utilizando Octave como nuestra herramienta.

Empecemos por lo básico, ¿qué es una matriz transpuesta? La transposición de una matriz implica convertir cada fila en una columna y, por supuesto, cada columna en una fila. Para ilustrarlo, consideremos la matriz M con dos filas y tres columnas.

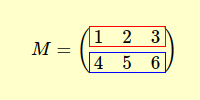
Su matriz transpuesta M^T tiene los elementos de cada fila dispuestos en columnas.

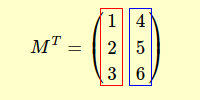
Para comprenderlo mejor, veamos un ejemplo práctico.

Primero, generemos una matriz rectangular con seis elementos.

>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6

Nuestra matriz M tiene dos filas y tres columnas.

$$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} $$

Para obtener la matriz transpuesta, simplemente escribe el nombre de la variable seguido por una comilla simple, es decir, M'

>> M'
ans =
1 4
2 5
3 6

Como alternativa, también puedes transponer la matriz con la función transpose(M)

>> transpose(M)
ans =
1 4
2 5
3 6

Ya sea con 'M' o con transpose(M), obtendrás la matriz transpuesta.

Nuestra matriz transpuesta es una matriz rectangular de 3x2, con las filas reordenadas en columnas

$$ M^T = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} $$

Un punto importante a recordar: La primera fila de la matriz inicial, compuesta por los elementos [1 2 3], ahora se ha convertido en la primera columna de la matriz transpuesta. Lo mismo ocurre con la segunda fila. La segunda fila [4 5 6] de la matriz inicial ahora se muestra como la segunda columna de la matriz transpuesta.