La rotación de una matriz en Octave

En esta lección, vamos a explorar el concepto de rotación de una matriz en Octave, ilustrándolo con ejemplos prácticos.

Primero, ¿qué entendemos por rotación de una matriz? Es un proceso por el cual una matriz gira en sentido horario (hacia la derecha) o antihorario (hacia la izquierda). Para ilustrarlo, si rotamos una matriz 90° en sentido horario, obtenemos el siguiente resultado:

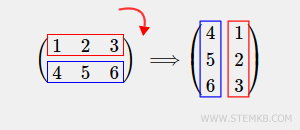
Comenzamos creando una matriz rectangular de 2x3:

>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6

A continuación, procedemos a rotar la matriz 90° en sentido antihorario.

Para ello, escribimos rot90(M,1)

>> rot90(M,1)
ans =
3 6
2 5
1 4

El resultado es la matriz inicial rotada 90° hacia la izquierda.

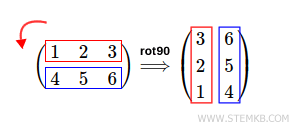
Es importante señalar que para obtener este resultado, también podríamos simplemente escribir rot90(M), ya que Octave asume por defecto que el segundo parámetro es igual a 1. La dirección por defecto es antihoraria (a la izquierda), que es la convención adoptada en matemáticas y física. Para rotar la matriz a la derecha, en cambio, debemos indicar un número negativo, como -1.

Si deseamos rotar la matriz 90° a la derecha, escribimos rot90 (M, -1), donde el segundo parámetro es un número entero negativo, es decir, -1

>> rot90(M,-1)
ans =
4 1
5 2
6 3

En este caso, el resultado es la matriz rotada 90° a la derecha.

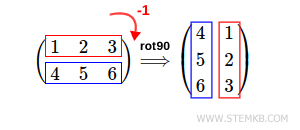
También es posible rotar la matriz 180° a la izquierda.

Para ello, escribimos rot90(M,2)

>> rot90(M,2)
ans =
6 5 4
3 2 1

El resultado es una doble rotación de 90° de la matriz a la izquierda.

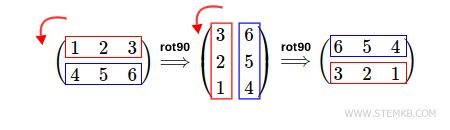
De manera similar, podemos rotar la matriz 180° a la derecha escribiendo rot90(M, -2), donde el segundo parámetro es un número entero negativo, es decir, -2

>> rot90(M,-2)
ans =
6 5 4
3 2 1

El resultado es una doble rotación de 90° de la matriz a la derecha.

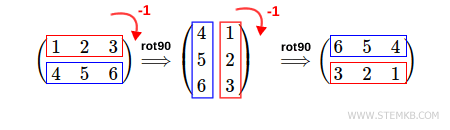
Podemos realizar cualquier número de rotaciones de la matriz utilizando la función rot90(M, n), donde el segundo parámetro indica el número de rotaciones a la izquierda (n> 0) o a la derecha (n <0).

Por ejemplo, para rotar la matriz 270° a la izquierda, escribimos rot90(M,3)

>> rot90(M,3)
ans =
4 1
5 2
6 3

El resultado es la matriz rotada tres veces 90° a la izquierda.

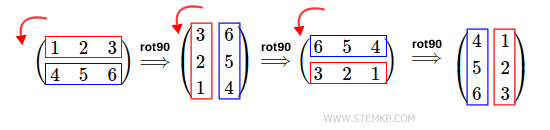
Para rotar la matriz 270° a la derecha, simplemente escribimos rot90(M,-3), indicando -3 como el segundo parámetro de la función.

Para rotar la matriz 360° a la izquierda, escribimos rot90(M,4)

>> rot90(M,4)
ans =
1 2 3
4 5 6

En este caso, obtenemos la matriz inicial, ya que hemos realizado cuatro rotaciones de 90° a la izquierda.

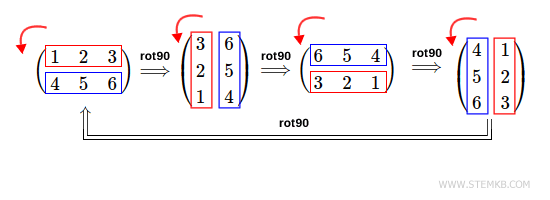
Espero que esta lección te haya proporcionado una comprensión clara de cómo rotar matrices en Octave.

Recuerda que la práctica es esencial para consolidar estos conceptos. ¡Sigue experimentando!