Matriz dispersa en Octave

En el presente tutorial en línea, te guiaré a través del proceso de creación de una matriz dispersa (sparse matrix) utilizando Octave.

Primero, definamos qué es una matriz dispersa y cuál es su utilidad. Cuando generamos una matriz de gran tamaño que contiene un alto número de ceros, estamos ocupando de manera innecesaria una considerable cantidad de la memoria de la computadora. Tomemos por caso una matriz diagonal, en la que sólo los valores en la diagonal principal son distintos de cero y todos los demás son ceros. $$ M = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ Para conseguir el mismo resultado sin consumir tanta memoria, puedes crear una matriz dispersa, en la que los ceros se comprimen.

Las matrices dispersas son especialmente útiles para crear matrices de identidad y matrices diagonales comprimidas.

La matriz de identidad dispersa

Permíteme mostrarte un ejemplo práctico.

Para crear una matriz de identidad, debes escribir eye(4)

>> eye(4)
ans =
Diagonal Matrix1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

Observa que en la matriz hay 12 ceros y 4 unos. Esto significa que una gran parte del espacio se encuentra ocupado por valores nulos, lo cual es innecesario.

Puedes obtener la misma matriz de identidad empleando una matriz dispersa. Para ello, utiliza el comando speye(4).

>> speye(4)
ans =
Compressed Column Sparse (rows = 4, cols = 4, nnz = 4 [25%])
(1, 1) -> 1
(2, 2) -> 1
(3, 3) -> 1
(4, 4) -> 1

La matriz dispersa sólo almacena las posiciones (fila, columna) que tienen valores no nulos, lo que resulta en un uso más eficiente del espacio de memoria.

Este es el motivo por el cual se denomina "dispersa" a este tipo de matriz.

Un detalle a tener en cuenta es que en la matriz dispersa, sólo se guarda información relevante. En una matriz de identidad, los valores nulos no tienen relevancia, por lo que se eliminan. Esto disminuye el espacio de memoria que se utiliza y acelera los cálculos con la matriz. Esto es especialmente útil cuando la matriz es de gran tamaño.

Ahora bien, puedes usar la matriz dispersa que acabas de crear en tus cálculos de la misma manera que usarías una matriz de identidad de 4x4.

Por ejemplo, podrías crear una matriz con 4 columnas.

>> M=[1 2 3 4;5 6 7 8; 9 0 1 2; 3 4 5 6]
M =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Ahora, multiplica la matriz M por la matriz de identidad.

>> M*eye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Después, multiplica la matriz M por la matriz de identidad dispersa.

>> M*speye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Como puedes ver, el resultado es el mismo.

En el segundo caso, sin embargo, se utiliza menos memoria y el tiempo de cómputo se reduce.

La Matriz Diagonal Dispersa

Para crear una matriz diagonal dispersa con valores distintos de 1, utiliza el comando spdiags().

>> spdiags([1;2;3],0,3,3)
ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 3 [33%])

(1, 1) -> 1
(2, 2) -> 2
(3, 3) -> 3

• El primer parámetro es un vector columna [1; 2; 3] que contiene los elementos de la diagonal.
• El segundo parámetro es el número índice de la diagonal, donde el número cero (0) corresponde a la diagonal principal.
• El tercer y cuarto parámetros son el número de filas (3) y de columnas (3) de la matriz dispersa.

El resultado es la matriz dispersa de una matriz diagonal 3x3.

$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{pmatrix} $$

Cómo definir una matriz dispersa con valores específicos

También puedes crear una matriz dispersa especificando únicamente los valores no nulos y sus correspondientes posiciones en la matriz.

Por ejemplo, crea una matriz dispersa con estos valores.

$$ M = \begin{pmatrix} 3 & 0 & 1 \\ 0 & 1 & 2 \\ 4 & 0 & 0 \end{pmatrix} $$

Primero, define un array con tantas filas como valores no nulos hay en la matriz.

Luego, en cada fila del array, escribe el número de fila, el número de columna y el valor del elemento no nulo.

>> v = [1 1 3; 1 3 1; 2 2 1; 2 3 2; 3 1 4]
v =
1 1 3
1 3 1
2 2 1
2 3 2
3 1 4

Observa cómo el primer elemento no nulo (3) se encuentra en la primera fila y columna (1,1), lo cual hace que la primera fila del vector sea 1 1 3. El segundo elemento no nulo (1) se encuentra en la primera fila en la tercera columna, por lo que la segunda fila del vector es 1 3 1. Y así sucesivamente.

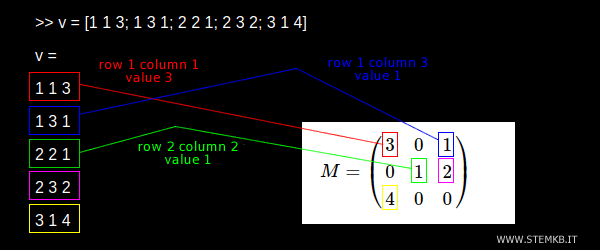
Para crear la matriz dispersa, utiliza la función spconvert()

>> spconvert(v)

El resultado es una matriz dispersa con los valores en las posiciones que has indicado.

ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 5 [56%])
(1, 1) -> 3
(3, 1) -> 4
(2, 2) -> 1
(1, 3) -> 1
(2, 3) -> 2

En el array que utilizas para construir la matriz dispersa, puedes definir los valores no nulos en cualquier orden.

Un detalle importante a tener en cuenta es que también puedes indicar múltiples valores para la misma posición en la matriz. Cuando una posición en el array se repite, Octave suma los valores sin dar error. Por ejemplo, puedes definir una matriz dispersa en la que indicas en la posición (1,1) el valor 2 y el valor 3. En la posición (1,1), Octave suma los dos valores 2 + 3 = 5.

Usando este método, también es posible crear una matriz dispersa con números complejos.